Unter dem Motto, dass das beste Gegenmittel gegen Angst die Beschäftigung mit dem Angstmacher ist, darf ich Euch einen Unterrichtsbehelf unseres Mitglieds Ernst vorstellen, mit der man das Verhalten einer Epidemie studieren kann.
Wachstumsmodelle
Wachstumsprozesse kann man modellieren, hier eine Auswahl:
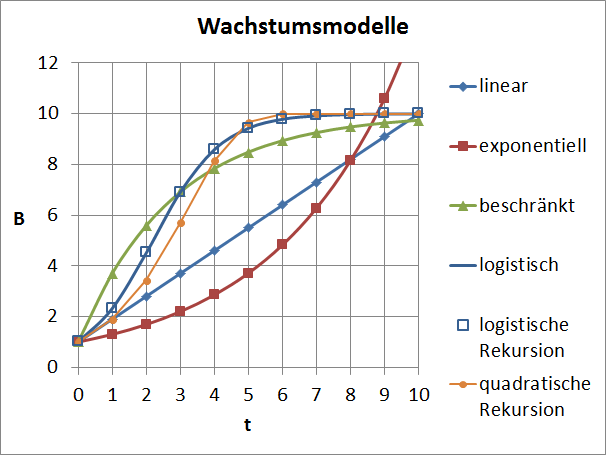
Im Zusammenhang mit Corona interessieren uns zwei dieser Modelle: das exponentielle Wachstum und das logistische Wachstum.
Exponentielles Wachstum
Was wir derzeit in Österreich beobachten, ist ein ungebremster Anstieg der Erkrankungsfälle. Da die Zuwachsrate von der Zahl der aktuell Erkrankten abhängt, ist dieser Zuwachs exponentiell, also vereinfacht gesagt, wenn die Zahl der Erkrankten 100 ist und die tägliche Zuwachsrate 30%, dann sind es am nächsten Tag 130 Erkrankte, und entsprechend sind es bei 1.000 Erkrankten am nächsten Tag 1.300.
Am Anfang der Epidemie schaut das recht harmlos aus, doch im Lauf der Zeit, wird einem bewusst, was genau „exponentiell“ bedeutet. Siehe dazu auch die Geschichte „Schachbrett und Reiskörner“ in der der Erfinder des Schachspiels durch Reiskörner am Schachbrett belohnt werden wollte, beginnend bei einem Reiskorn am ersten Feld und immer die doppelte Menge auf dem jeweils nächsten Feld. Es stellte sich bald heraus, dass niemand so reich ist, den Lohn zu bezahlen.
Setzt man das in dieser Form fort, würde man nach 89 Tagen die 10-Millionen-Grenze an Erkrankten übersteigen, aber so viele Österreicher gibt es gar nicht. Daher passt die Exponetialfunktion auch nur für den anfänglichen Verlauf einer Epidemie.
Logistisches Wachstum
Ein Virenträger kann nur gesunde Menschen anstecken aber nicht solche, die ohnehin schon angesteckt sind oder aus einem anderen Grund immun sind und daher hat die reale Wachstumskurve einen Wendepunkt und verflacht danach. Das ist die logistische Verteilung. (Im Bild oben blaue Kurve mit quadratischen Markierungen)
Zuwachsrate
Die Zuwachsrate pro Tag in Österreich liegt derzeit bei etwa 30-40% und die Zahl der Erkrankten verdoppelt sich alle 2 bis 3 Tage.
Die Zuwachsrate ist eine Funktion des sozialen Verhaltens, also eine große Nähe zu Menschen und viele Kontakte bedingen eine hohe Zuwachsrate, eine geringe Nähe und wenig Kontakte eben eine geringere. Das Virus selbst hat auch einen starken Einfluss. Masernviren sind viel kleiner als Corona und schweben lange in der Luft und daher sind sie viel ansteckender als die Corona-Viren, die früh zu Boden sinken.
Isolation
Die verordnete Isolation, das Abstandhalten und das Händewaschen haben zur Folge, dass die Zuwachsrate der Erkrankungen kleiner wird und dass es länger dauert, bis sich die Zahl der Erkrankten verdoppelt. Das ändert aber nichts daran, dass es zu einer ständigen Zunahme der Erkrankten kommt.
Durch die nun geringere Zuwachsrate verflacht die Kurve, aber das ändert nichts an ihrem prinzipiellen Verlauf, dass also irgendwann alle Menschen erkrankt sein werden.
Gesundung
Dem Ansteckungsverlauf überlagert sich aber ein Gesundungsverlauf und leider auch eine Todesrate, von der wir hoffen, dass sie gering sein möge. Nachdem die Epidemie eingesetzt hat, gesunden die Erkrankten wieder nach einiger Zeit (im Bild unten nach 14 Tagen) und daher ist die Zahl der tatsächlich Erkrankten nicht mehr nur die der Neuerkrankungen, sondern abzüglich der bereits Gesundeten. Und das ergibt eine Glockenkurve, die die zu einem bestimmten Zeitpunkt erkrankten Menschen beschreibt.
Mit der Isolation verringert sich das Maximum des Verlaufs aber die Dauer der Epidemie vergrößert sich. Man hofft mit dieser Maßnahme mit der Zahl der verfügbaren Intensivbetten auszukommen. Die Isolation erspart uns aber nicht die Ansteckung, sie schiebt sie im Einzelfall nur hinaus.
Interaktives Modell
TGM-Kollege Ernst hat mit seiner Klasse diese Verläufe in einem Mathematikprogramm modelliert. Das Programm ist wunderbar interaktiv und man kann die Wirkung aller Parameter über Schieberegler verändern.
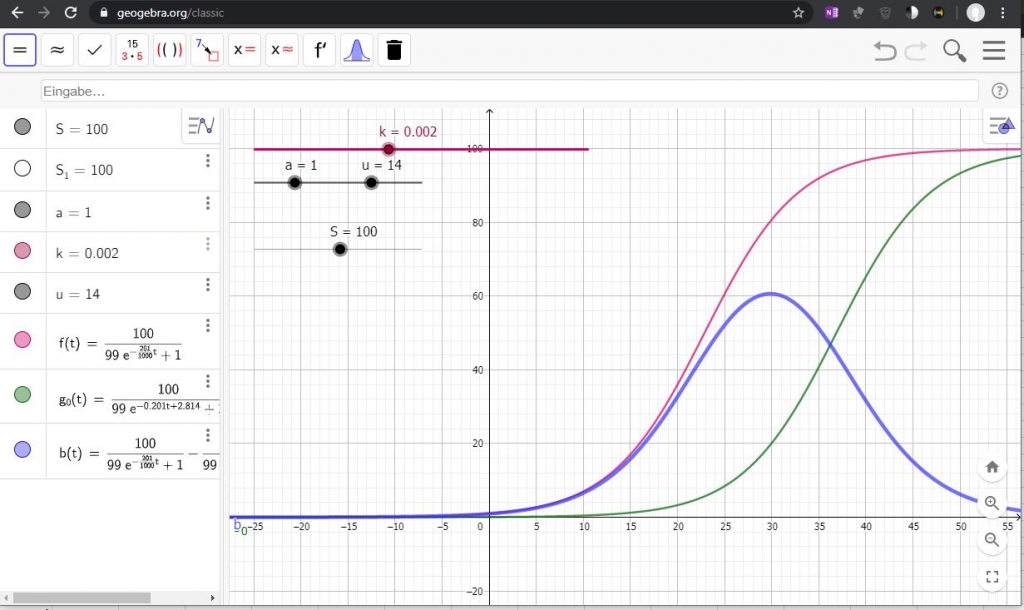
rot: Erkrankungen, grün: Gesundungen, blau: Erkrankte
S … Population, Sättigungsgrenze in %
a … Anzahl der Infizierten am Beginn in% von S
k … Konstante für die Ansteckungsgefahr, bei geringeren Sozialkontakten wird k kleiner!
u … Durchschnittliche Verlaufsdauer einer Erkrankung in Tagen
Mit den Schiebereglern links oben im Diagramm kann man die Parameter verändern und damit das Verhalten der Verläufe verändern. Man sieht also, wie sich blaue Kurve (Zahl der aktuellem Erkrankungen) verflacht, wenn man die Zahl der Sozialkontakte k verkleinert.
Zwischen Theorie und Realität
Diese Kurven sind natürlich nur Modelle. Die Grundannahme ist S=100%, (S ist das Maß für die Sättigung) was bedeutet, dass die Neuerkrankungen erst dann verschwinden, wenn tatsächlich alle Menschen erkrankt und wieder gesundet sind. Dieses S ist die so genannte „Herdenimmunität“, also ein Prozentsatz an bereits erkrankten und wieder gesundeten Menschen, die durch die Erkrankung immunisiert sind.
Dass man nicht darauf warten muss, bis tatsächlich 100% der Bevölkerung erkrankt sind, sieht man am Verlauf in Wuhan. Warum diese Trendumkehr – also das Absinken der Zahl der Erkrankten – schon viel früher stattfindet, wissen hoffentlich die Virologen.
Handhabung
Um dieses Programm zu benutzen, muss man nichts installieren. Man besucht die Seite
https://www.geogebra.org/classic
Nun lädt man sich die Datei Corona_logistisch.zip aus dem Anhang dieser Seite und entpackt sie zu Corona_logistisch.ggb.
Die aus dem ZIP-Archiv entpackte ZIP-Datei zieht man in den Entwurfsbereich. Danach kann man die Parameter S, a, k, u entweder als Zahlenwert eingeben oder mit den Schiebereglern verändern. Jede Kurve und jeder Schieberegler kann mit den bunten Buttons links ein- und ausgeschaltet werden.
Franz war pensionierter HTL Lehrer (TGM), Präsident von ClubComputer, Herausgeber der Clubzeitung PCNEWS und betreute unser Clubtelefon und Internet Support. Er war leidenschaftlicher Rapid Wien Fan. Er ist leider Anfang Jänner 2024 nach langer schwerer Krankheit verstorben.

Neueste Kommentare