Datenstrukturen
Ein Computer hat die Aufgabe, eingegebene Daten zu verarbeiten. Im Gegensatz zum Menschen, der in der Lage ist, komplexe Zahlen, Wörter und Realbilder aufzunehmen und zu verarbeiten, selbständig Gedanken zu formen und sich frei auszudrücken, kann der Mikrocomputer lediglich zwei Zustände unterscheiden:
Entweder es fließt Strom, oder es fließt eben keiner.
Mit diesem „Wissen“ muss der Computer alles das zustande bringen, was wir von ihm erwarten. Alle Daten müssen in einer speziellen Form dargestellt werden, um für den Computer „verständlich“ zu sein. Wir betrachten daher zunächst Möglichkeiten, Zahlen darzustellen. Dabei werden wir ein Zahlensystem kennen lernen, das nur zwei Ziffern aufweist und als Grundlage für alle Vorgänge im Computer dient.
Zahlensysteme
Heute benutzen wir üblicherweise zur Darstellung von Zahlen das so genannte Dezimalsystem. Der Name „dezimal“ leitet sich vom lateinischen Wort „decem“ = 10 ab; 10 stellt die Basis dieses Zahlensystems dar.
Zahlen im Zehnersystem bestehen aus den Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9. Je nachdem, an welcher Stelle diese Ziffern stehen, haben sie verschiedene Werte, z.B.
358 = 3·102 + 5·101 + 8·100
Jede Stelle entspricht also einer Potenz der Basis 10.
Für einen Computer wäre es technisch sehr kompliziert, 10 verschiedene Schaltungszustände (etwa 0 Volt, 1 Volt, … 10 Volt) herzustellen, da durch Übertragungsfehler benachbarte Zustände (z.B. 5 und 6 Volt) nicht mehr unterscheidbar wären. Daher bedient man sich des einfachsten Zahlensystems, das es überhaupt gibt, des Binär- oder Dualsystems.
Wie der Name schon sagt, gibt es hier nur zwei mögliche Schaltungszustände, die verschieden bezeichnet werden können:
wahr – falsch
0 – 1
ja – nein
High – Low usw.
Für eine mathematische Behandlung eignen sich die Bezeichnungen 0 und 1. Es gibt hier also nur zwei Ziffern. Die beiden Schaltungszustände werden technisch bei TTL-Technik durch 0 Volt („low“) und 5 Volt („high“) dargestellt, wobei natürlich auch hier Spannungsbereiche verwendet werden. (Also etwa: low = (0…0,9) V, high = (2,4…5) V.) Eine Binärziffer hat den Informationsgehalt 1 bit (= 1 binary digit, 1 binäre Einheit).
Die Wertberechnung erfolgt wie im Dezimalsystem, nur mit der Basis 2:
1011 = 123 + 022 + 121 + 120
Welche Zahl im Zehnersystem entspricht nun 10112? Wir brauchen nur die Darstellung in der rechten Spalte auszurechnen und erhalten 1110. (Die Basis schreibt man meist tiefgestellt nach der Zahl; statt 9710 ist auch die Bezeichnung 97d üblich, statt 10112 schreibt man auch 1011b.)
Umrechnen von Dezimal- in Dualzahlen
Dazu kann man folgendes einfache Schema benutzen: Man dividiert durch die größte vorkommende Zweierpotenz, das Ergebnis schreibt man an. Der Rest wird wieder durch die größte enthaltene Zweierpotenz dividiert etc.
Beispiel: Gesucht ist die Binärdarstellung von 17310.
210 = 1024 29 = 512 28 = 256 27 = 128 173 : 128 = 1, 45 R 26 = 64 45 : 64 = 0, 45 R 25 = 32 45 : 32 = 1, 13 R 24 = 16 13 : 16 = 0, 13 R 23 = 8 13 : 8 = 1, 5 R 22 = 4 5 : 4 = 1, 1 R 21 = 2 1 : 2 = 0, 1 R 20 = 1 1 : 1 = 1, 0 R
Die Rechnung ergibt also:
17310 = 1010 11012
Diese Zahl hat also einen Informationsgehalt von 8 bit, da man 8 Binärziffern zu ihrer Darstellung braucht. (Die Unterteilung in Vierergruppen dient der Übersichtlichkeit.)
Ein anderer bekannter Algorithmus funktioniert folgendermaßen: Man dividiert die Dezimalzahl fortwährend durch 2 und notiert die Reste in umgekehrter Reihenfolge.
Beispiel: Gesucht ist die Binärdarstellung von 17310.
173 : 2 = 86, 1 R
86 : 2 = 43, 0 R
43 : 2 = 21, 1 R
21 : 2 = 10, 1 R
10 : 2 = 5, 0 R
5 : 2 = 2, 1 R
2 : 2 = 1, 0 R
1 : 2 = 0, 1 R
17310 = 1010 11012
Addition von Binärzahlen
Binärzahlen werden genauso addiert wie Dezimalzahlen, nur dass die Rechenregeln wesentlich einfacher sind:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10 (weil 102 = 210)
Das heißt: Bei Addition zweier Einser muss man einen Übertrag 1 berücksichtigen.
Beispiel:
1101
+ 1011
——————
11000
Man sieht, dass Dualzahlen sehr viel mehr Stellen benötigen als Dezimalzahlen. Ein Programmierer, der die Maschinensprachebefehle auf diese Art eingeben müsste, würde bald verzweifeln.
Daher fasst man jeweils 4 Stellen zusammen – es ergibt sich das Hexadezimalsystem. Es beruht auf der Basis 16 und benötigt 16 Ziffern zur Zahlendarstellung:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Die „Ziffern“ A bis F stehen dabei für die Werte 10 bis 15.
Es gibt verschiedene Schreibweisen für Hexadezimalzahlen:
- 2A316 (Mathematik)
- 2A3h (Assembler)
- $2A3 (Assembler)
- X’2A3’ (Assembler)
- 0x2A3 (C, C++, C#, Java, JavaScript, PHP, …)
- 2A3#16# (ADA)
Eine Zahl 2A316 bedeutet daher:
2A3 = 2∙162 + 10∙161 + 3∙160
Die Umrechnung ergibt:
2∙256 + 10∙16 + 3 = 675
Andere Umrechnung (Horner-Schema):
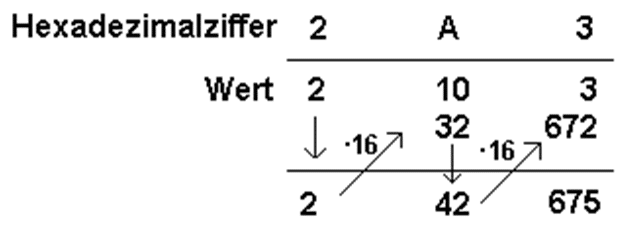
Zahlendarstellung; Bit und Byte
Die Informationen werden im Inneren des Computers als Ketten von binären Informationseinheiten = Bit (1 bit = 1 b = engl. binary digit, binäre Einheit) gespeichert. Eine binäre Einheit ist die Entscheidung 0/1 oder kein Strom/Strom usw.
8 binäre Einheiten werden als 1 Byte = 1 B (engl. „by eight“) bezeichnet.
Für größere Informationsmengen benützt man Vielfache der Einheit Byte. Da es bis 1996 keine speziellen Einheitenvorsätze für Zweierpotenzen gab, hat es sich verbreitet, die SI-Präfixe im Zusammenhang mit Speicherkapazitäten zur Bezeichnung von Zweierpotenzen zu verwenden (mit Faktor 210 = 1024 statt 1000), z.B.:
1 Kilobyte (kB) = 1024 Byte, 1 Megabyte (MB) = 1024 Kilobyte = 1024 · 1024 Byte = 1.048.576 Byte
Diese binäre Verwendung der SI-Präfixe wurde 1986 von der IEEE auch in einem Glossar dokumentiert.
In Kontexten, wo Zweierpotenzen keine besondere Bedeutung haben, z.B. bei Datenübertragungsraten, Speicherkapazitäten von Festplatten, DVD-Rohlingen usw., werden die SI-Präfixe jedoch häufig entsprechend ihrer Definition im SI-System als Dezimalpräfixe verwendet, was zu nominal größeren Zahlenwerten führt, z.B.:
1 Kilobyte (kB) = 1000 Byte, 1 Megabyte (MB) = 1000 Kilobyte = 1000 · 1000 Byte = 1.000.000 Byte
Vereinzelt kommen auch Mischformen vor, z. B. bei der Speicherkapazität einer 3,5“–Diskette: 1,44 MB = 1440 KB = 1440 x 1024 Byte.
Um Mehrdeutigkeiten zu vermeiden, schlug die IEC 1996 neue Einheitenvorsätze vor, die nur in der binären Bedeutung verwendet werden sollten. (siehe Tabelle unten)
| Name (Symbol) | SI-Präfixe | Unter-schied | Name (Symbol) | Binärpräfixe | |
| Kilobyte (kB) | 103 Byte = 1.000 Byte | 2,4 % | Kibibyte (KiB) | 210 Byte = 1.024 Byte | |
| Megabyte (MB) | 106 Byte = 1.000.000 Byte | 4,9 % | Mebibyte (MiB) | 220 Byte = 1.048.576 Byte | |
| Gigabyte (GB) | 109 Byte = 1.000.000.000 Byte | 7,4 % | Gibibyte (GiB) | 230 Byte = 1.073.741.824 Byte | |
| Terabyte (TB) | 1012 Byte = 1.000.000.000.000 Byte | 10,0 % | Tebibyte (TiB) | 240 Byte = 1.099.511.627.776 Byte | |
| Petabyte (PB) | 1015 Byte = 1.000.000.000.000.000 Byte | 12,6 % | Pebibyte (PiB) | 250 Byte = 1.125.899.906.842.624 Byte | |
| Exabyte (EB) | 1018 Byte = 1.000.000.000.000.000.000 Byte | 15,3 % | Exbibyte (EiB) | 260 Byte = 1.152.921.504.606.846.976 Byte | |
| Zettabyte (ZB) | 1021 Byte = 1.000.000.000.000.000.000.000 Byte | 18,1 % | Zebibyte (ZiB) | 270 Byte = 1.180.591.620.717.411.303.424 Byte | |
| Yottabyte (YB) | 1024 Byte = 1.000.000.000.000.000.000.000.000 Byte | 20,9 % | Yobibyte (YiB) | 280 Byte = 1.208.925.819.614.629.174.706.176 Byte |
Darstellung ganzer Zahlen
Für die interne Zahlendarstellung bestehen mehrere Möglichkeiten:
Darstellung von Dezimalzahlen durch ziffernweise duale Codierung („unechte“ Dualzahlen)
Verschlüsselt man jede der zehn Dezimalziffern einzeln als Zeichen, so benötigt man ein Byte pro Ziffer. Da in Wirklichkeit aber nur 4 bit verwendet werden, lässt man die ersten 4 bit des Byte einfach auf „1111“ gesetzt und codiert die Ziffer binär in der zweiten Hälfte des Bytes:
"0" ..... 1111 0000
"1" ..... 1111 0001
"2" ..... 1111 0010
..... .....
"8" ..... 1111 1000
"9" ..... 1111 1001
Die linke Bytehälfte wird als „Zone“ bezeichnet und ist redundant; diese Art der Speicherung heißt danach gezonte Zahlendarstellung und ist vor allem in Großrechnern verbreitet.
Die Zahl 325 wird z.B. als
1111 0011 1111 0010 1111 0101
oder hexadezimal geschrieben als
F3 F2 F5
gespeichert.
Zur Darstellung eines eventuellen negativen Vorzeichens wird üblicherweise das hexadezimale F des am weitesten rechts stehenden Bytes durch D16 = 11012 ersetzt. Die Zahl -97 würde z.B. also als
1111 1001 1101 0111
oder
F9D716
dargestellt.
In dieser Form können Zahlen zwar einfach (nämlich zeichenweise) ein- und ausgegeben werden (zur Umwandlung in den ANSI- oder ASCII-Code brauchen nur die ersten beiden bits jedes Bytes auf 00 gesetzt werden), ein Rechnen ist so jedoch unmöglich. Das bedeutet, dass gezont gespeicherte Zahlen vor jeder Rechenoperation in eine der im Folgenden beschriebenen Formen umgewandelt werden müssen (und danach wieder zurückgewandelt).
Um Rundungsfehler bei der Umrechnung von Dezimal- in Binärzahlen und umgekehrt zu vermeiden, kann man Dezimalzahlen auch so umwandeln, dass man jede Stelle extra in eine Binärzahl umwandelt (BCD = binary coded decimal). Für jede Stelle der Dezimalzahl benötigt man genau ein Halbbyte oder Nibble = 4 bit.
Beispiel:
9510 = ?
910 = 10012
510 = 01012
9510 = 1001 0101 BCD
Offensichtlich genügt auch ein halbes Byte pro Ziffer; eine solche Speicherung heißt wegen der Speicherplatzersparnis gepackte Zahlendarstellung:
"325"
ergibt binär
0000 0011 0010 0101 = 032516
Für ein eventuelles Vorzeichen ist nun freilich ein eigenes Halbbyte nötig, dass meist rechts von der Einerziffer angeordnet wird. Abgesehen davon und von einer eventuell notwendigen führenden Null, beträgt die Speicherplatzersparnis 50%.
Großrechner können meist mit gepackten Zahlen hardwaremäßig rechnen.
Darstellung von Dezimalzahlen als Ganzes in rein dualer Form („echte“ Dualzahlen)
Diese Zahlendarstellung verwendet der Rechner vor allem bei der Bestimmung von Speicheradressen.
Da in der gepackten Darstellung immer noch 6 der 16 Codierungsmöglichkeiten in einem Halbbyte „verschenkt“ werden, muss es eine noch kompaktere Form geben: die ganze Zahl wird einfach als Dualzahl gespeichert, wobei üblicherweise 2, 4 oder 8 Byte für die Codierung einer Zahl verwendet werden. So hat jede beliebige Bitkombination genau eine Dezimalzahl als Entsprechung; die Redundanz ist – abgesehen von führenden Nullen zur Ergänzung auf Halbwort, Wort oder Doppelwort – gleich Null. Zur Darstellung von ganzen Zahlen (Bezeichnung meist „integer“) werden oft 2 Bytes verwendet. Die Zahlen bis 216-1 = 65wären also problemlos darstellbar.
Darstellung von negativen Zahlen
Dabei verzichtet man zugunsten des Vorzeichens auf 1 bit:

Vorzeichendarstellung: ein Bit (zum Beispiel das höchstwertige) wird als Vorzeichen definiert (0 entspricht +, 1 entspricht –).
„Zweierkomplement“ = NOT(Dualzahl) + 1
Dazu berechnet man aus der gegebenen positiven Binärzahl zunächst die „bitweise Negation“ (siehe Kap. 22: Logische Verknüpfungen), indem man die Werte 0 und 1 „austauscht“. Anschließend addiert man zu dieser Zahl den Wert 1.
Das bedeutet: alle Zahlen von –32bis +32können exakt dargestellt werden.
Beispiel
0000 0001 dezimal 1 1111 1110 NOT 1 (Einer-Komplement) 1111 1111 +1 (Zweier-Komplement)
Die Subtraktion von Binärzahlen kann daher durch Addition des Komplements erfolgen.
Die übliche Darstellung von negativen Zahlen ist die Zweier-Komplement-Darstellung.
Achtung: Für die Addition einer positiven Dualzahl mit einem Zweier-Komplement müssen folgende Regeln eingehalten werden:
- Beide Zahlen müssen gleich lang dargestellt werden (z.B. beide Zahlen mit 8 Stellen, aber natürlich mindestens soviele, wie die größere Zahl benötigt)
- Das Ergebnis ist genauso lang wie die beiden Einzelzahlen. Sollte eine zusätzliche Stelle beim Addieren zustande kommen, so muss diese vernachlässigt werden.
Festkommadarstellung
Zur dualen Darstellung nicht ganzer Dezimalzahlen wird hier eine fixe Anzahl von Nachkommastellen verwendet. Die rechts vom Dualpunkt stehenden Dualziffern werden mit negativen Potenzen von 2 gewichtet, also mit 0.5, 0.25, 0.125, 0.0625 usw.
Beispiele
101.112 = 5.7510
11111.0012 = 31.12510
Die Umwandlung einer nicht ganzen Dezimalzahl in das Dualsystem kann so erfolgen, dass zuerst der ganzzahlige Anteil durch fortlaufende Division durch 2 umgerechnet wird und danach der gebrochene Anteil durch fortlaufende Multiplikation mit 2. Vom Ergebnis jeder Multiplikation wird der ganzzahlige Anteil abgeschnitten – er stellt die zugehörige duale Ziffer dar.
Am folgenden Beispiel sieht man sehr schön, dass selbst einfache Dezimalbrüche auf unendliche (natürlich periodische!) Dualbrüche führen. Die Darstellung nicht-ganzer Dezimalzahlen ist daher im Dualsystem (bei limitierter Stellenanzahl) nur in Ausnahmefällen exakt möglich. Im allgemeinen wird daher die kleinste darstellbare Stelle gerundet.
Beispiel: Umwandeln von 25.7 ins Dualsystem
25 : 2 = 12
12 : 2 = 6
6 : 2 = 3
3 : 2 = 1
1 : 2 = 0
Rest: 1 0 0 1 1
à 2510 = 110012
0.7 x 2 = 1.4
0.4 x 2 = 0.8
0.8 x 2 = 1.6
0.6 x 2 = 1.2
abgeschnitten: 1 0 1 1
à 0.710 = 0.1011...
(genauer: 0.101100110011002 = 0.1011002)
à 25.710 = 11001.10112
Gleitkommadarstellung
Für größere Zahlenbereiche benützt der Computer die Gleitkommadarstellung, hier erläutert an der Dezimalzahl
1 700 000.
| 1700 000 = | 0,17 | 10 | 7 |
| Mantisse | Basis | Exponent |
Es müssen nur Mantisse und Exponent gespeichert werden (als ganze Zahlen! – also m=17, e=7). Auch der Exponent kann ein negatives Vorzeichen haben. (Vereinbarung: Die erste Stelle rechts vom Komma muss ungleich Null sein!) Wie man sieht, ist die Speicherung einer Gleitkommazahl nur mit einer bestimmten Genauigkeit möglich. Dadurch ergeben sich bei Division, Multiplikation und anderen Rechenvorgängen höherer Ordnung Fehler durch Abschneide- und Rundungsvorgänge; allerdings bleibt der maximale prozentuelle Fehler gleich.
Gleitkommazahlen werden üblicherweise im IEEE-Format (IEEE = Institute of Electrical and Electronics Engineers) dargestellt:
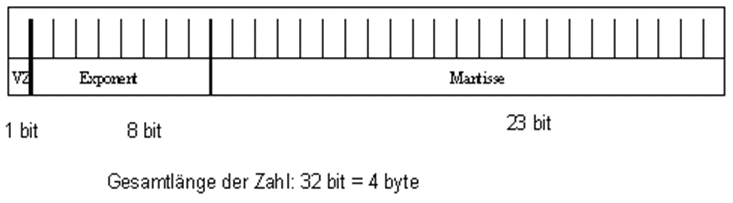
Es ist daher immer notwendig, die zur Verfügung stehende Genauigkeit mit einzugeben.
Die reellen Zahlen liegen bekanntlich unendlich dicht auf der Zahlengeraden. Zum Unterschied davon können mit einer endlichen Anzahl von Bits nur endlich viele Zahlen dargestellt werden. Dieses Dilemma versucht man mit der Gleitkommadarstellung zu entschärfen – es bleibt aber im Allgemeinen ein Fehler bei der Abbildung einer reellen Zahl auf eine computerintern dargestellte Zahl!
Um alle Zahlen, also auch sehr große und sehr kleine, einheitlich darstellen zu können, speichert man die Zahl in zwei Teilen: die Mantisse gibt die geltenden Ziffern an, der Exponent einen Skalierungsfaktor, z.B.:
0.0000123 = 123 * 10-7
Mantisse und Exponent sind ganze Zahlen, können also auch negativ sein.
Die Darstellung ist allerdings nicht eindeutig:
123 * 10-7 = 1230 * 10-8 = ...
Deshalb setzt man eine normalisierte Darstellung ein, bei der der Exponent so gewählt wird, dass die Mantisse kleiner als Eins ist und die erste Stelle nach dem Dezimalpunkt von Null verschieden ist. Die obige Zahl wird also normalisiert als
0.123 * 10-4
dargestellt. Man braucht dann nur die Nachkommastellen der Mantisse und den Exponenten speichern, also:
+123 -4
Im Dualsystem wird natürlich eine Zweierpotenz als Skalierungsfaktor verwendet; sowohl Mantisse als auch Exponent werden dual dargestellt.
Beispiel
5.7510
= 101.112 = 101.11 * 20 = 0.10111 * 23
+10111 +11
Die Genauigkeit der Zahlendarstellung im Gleitkommaformat wird durch die Länge der Mantisse bestimmt. Da sich durch m bit genau m/ld 10 Dezimalziffern darstellen lassen, ist die Gleitkommadarstellung mit einer Mantisse der Länge m auf m/ld 10, das ist ungefähr 0,3 * m Dezimalstellen genau.
Oft bieten Computer eine Darstellungsart mit einer um ein Wort verlängerten Mantisse an; dies wird als „doppelte Genauigkeit“ bezeichnet, was allerdings untertrieben ist. Die Norm „IEEE Standard-754“ definiert seit 1985 verschiedene empfohlene Gleitkommadarstellungen mit 23-Bit- oder 52-Bit Mantisse (plus Vorzeichen) und 8-Bit- bzw. 11-Bit-Exponent (inklusive Vorzeichen), allerdings dual normalisiert auf 1. … an Stelle von 0. …
Die betragsmäßig größte und kleinste darstellbare Zahl wird durch den Exponenten bestimmt. Mit 8 Bit langen Exponenten (inklusive codiertem Vorzeichen) bewegt man sich im Bereich von ± 2±127, also etwa ±10±38.
Die Rundungsproblematik beim Rechnen mit Gleitkommazahlen ist Gegenstand eines eigenen Zweiges der Mathematik, der numerischen Mathematik, zu der es umfangreiche Literatur, diverse Fachzeitschriften und vor allem viele Softwarepakete gibt.
Die Prozessoren der frühen Personal-Computer, die Intel 8086, 80286 und 80386 waren nicht in der Lage mit Gleitkommazahlen zu rechnen. „Mathematische Co-Prozessoren“ der Type 8087, 80287 und 80387 ergänzten jeweils genau diese Fähigkeit. Auch der Prozessor 80486 war in einer Variante mit Gleitkommarechnung als 80486DX bzw. ohne als 80486SX erhältlich. Erst ab der Pentium-Generation ist die Gleitkomma-Arithmetik immer inkludiert – und zwar zusätzlich zu zwei Rechenwerken für ganzzahlige Arithmetik, die alle parallel arbeiten.
Die Rechenleistung von Computern für technische Aufgabenstellungen wird oft in Flops gemessen: floating-point operations per second. Megaflops sind daher Millionen Gleitkommaoperationen pro Sekunde.
Codes
Codes für Zeichen und Befehle
ASCII
ASCII = American Standard Code for Information Interchange.
Ursprünglich war der ASCII-Code ein 7 bit-Code, das bedeutet, für ein ASCII-Zeichen wurde eine sieben bit lange „Codenummer“ vergeben. Mit 7 bit sind also insgesamt 128 Zeichen codierbar.
ASCII wurde im Jahr 1967 erstmals als Standard veröffentlicht und im Jahr 1986 zuletzt aktualisiert. Die Zeichenkodierung definiert 128 Zeichen, bestehend aus 33 nicht-druckbaren sowie 95 druckbaren.
Der von PCs heute verwendete Standard verwendet jedoch einen 8 bit-Code. Für einen ASCII-Wert steht 1 Byte zur Verfügung. Damit sind 256 verschiedene Zeichen codierbar.
ASCII-Werte kleiner als 32 stehen für Steuerzeichen. 65 bedeutet ‘A’, 66 bedeutet ‘B’ usw.
Beispiel
A 65 = 0 1 0 0 0 0 0 1 Zahlenwert 27 26 25 24 23 22 21 20
Im ASCII sind die Zeichen 0 bis 127 laut Tabelle genormt. Dieser Code wird von praktisch allen Rechnern (außer IBM-Großrechenanlagen) verwendet. Die ASCII-Zeichen 127 bis 255 sind nicht genormt. Die entsprechenden Zeichen findet man in Tabellen.
Die Zeichen mit den Nummern 0 bis 31 sind Steuerzeichen, die (im Allgemeinen) nicht gedruckt werden können und in den Listen nicht dargestellt sind.
Ein Zeichen mit beliebiger Nummer wird so eingegeben: «Alt»-Taste drücken, gedrückt lassen, Nummer auf dem nummerischen Tastenblock eingeben, «Alt»-Taste loslassen.
Folgende druckbare Zeichen werden unter MS-DOS oder in einem MS-DOS-Fenster verwendet. Je nach Sprachgebiet können unterschiedliche Codetabellen gewählt werden.
Codetabelle 437 Amerikanisch
..│ 0 1 2 3 4 5 6 7 8 9 A B C D E F│/..
──┼────────────────────────────────┼───
00│ ☺ ☻ ♥ ♦ ♣ ♠ ● ◘ ○ ◙ ♂ ♀ ♪ ♫ ☼│000
10│ ► ◄ ↕ ‼ ¶ § ▬ ↨ ↑ ↓ → ← ∟ ↔ ▲ ▼│016
20│ ! " # $ % & ' ( ) * + , - . /│032
30│ 0 1 2 3 4 5 6 7 8 9 : ; < = > ?│048
40│ @ A B C D E F G H I J K L M N O│064
50│ P Q R S T U V W X Y Z [ \ ] ^ _│080
60│ ` a b c d e f g h i j k l m n o│096
70│ p q r s t u v w x y z { | } ~ │112
80│ Ç ü é â ä à å ç ê ë è ï î ì Ä Å│128
90│ É æ Æ ô ö ò û ù ÿ ö ü ¢ £ ¥ P ƒ│144
A0│ á í ó ú ñ Ñ ª º ¿ ⌐ ¬ ½ ¼ ¡ « »│160
B0│ ░ ▒ ▓ │ ┤ ╡ ╢ ╖ ╕ ╣ ║ ╗ ╝ ╜ ╛ ┐│176
C0│ └ ┴ ┬ ├ ─ ┼ ╞ ╟ ╚ ╔ ╩ ╦ ╠ ═ ╬ ╧│192
D0│ ╨ ╤ ╥ ╙ ╘ ╒ ╓ ╫ ╪ ┘ ┌ █ ▄ ▌ ▐ ▀│208
E0│ α β Γ Π Σ σ μ γ Φ Θ Ω δ 8 Ø ε n│224
F0│ = ± = = ( ) ÷ ~ ° ∙ • V n ² ■ │240
──┼────────────────────────────────┼───
./│ 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1│...
/.│ 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5│...
Codetabelle 850 Mehrsprachig (Lateinisch I)
..│ 0 1 2 3 4 5 6 7 8 9 A B C D E F│/..
──┼────────────────────────────────┼───
00│ ☺ ☻ ♥ ♦ ♣ ♠ ● ◘ ○ ◙ ♂ ♀ ♪ ♫ ☼│000
10│ ► ◄ ↕ ‼ ¶ § ▬ ↨ ↑ ↓ → ← ∟ ↔ ▲ ▼│016
20│ ! " # $ % & ' ( ) * + , - . /│032
30│ 0 1 2 3 4 5 6 7 8 9 : ; < = > ?│048
40│ @ A B C D E F G H I J K L M N O│064
50│ P Q R S T U V W X Y Z [ \ ] ^ _│080
60│ ` a b c d e f g h i j k l m n o│096
70│ p q r s t u v w x y z { | } ~ │112
80│ Ç ü é â ã à Á ç ê Ê è Í Ô ì à Â│128
90│ É À È ô õ ò Ú ù Ì Õ Ü ¢ £ Ù P Ó│144
A0│ á í ó ú ñ Ñ ª º ¿ Ò ¬ ½ ¼ ¡ « »│160
B0│ ░ ▒ ▓ │ ┤ ╡ ╢ ╖ ╕ ╣ ║ ╗ ╝ ╜ ╛ ┐│176
C0│ └ ┴ ┬ ├ ─ ┼ ╞ ╟ ╚ ╔ ╩ ╦ ╠ ═ ╬ ╧│192
D0│ ╨ ╤ ╥ ╙ ╘ ╒ ╓ ╫ ╪ ┘ ┌ █ ▄ ▌ ▐ ▀│208
E0│ α β Γ Π Σ σ μ γ Φ Θ Ω δ 8 Ø ε n│224
F0│ = ± = = ( ) ÷ ~ ° ∙ • V n ² ■ │240
──┼────────────────────────────────┼───
./│ 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1│...
/.│ 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5│...
ISO 8859
ISO 8859 ist die gültige internationale ISO-Norm (International Standards Organization) für Zeichensätze. Es gibt derzeit 10 Varianten für die folgenden Sprachgebiete:
- 8859-1: Westeuropa, Lateinamerika; auch: Latin-1
- 8859-2: Osteuropa; auch: Latin-2
- 8859-3: Südosteuropa, Malta, Esperanto
- 8859-4: Skandinavien, Baltikum
- 8859-5: Kyrillisch
- 8859-6: Arabisch
- 8859-7: Griechisch
- 8859-8: Hebräisch
- 8859-9: wie 8859-1, jedoch Türkisch statt Isländisch
- 8859-10: Lappland, Eskimo usw.
- 8859-15: Westeuropa, Lateinamerika (~ ISO 8850-1 mit €-Zeichen)
- 8859-16: Osteuropa (~ ISO 8850-2 mit €-Zeichen)
Der in unseren Breiten zum Einsatz kommende Zeichensatz ISO 8859-1 ist aus der folgenden Tabelle ersichtlich. Steuerzeichen – das sind Zeichen, die zur Steuerung des Ausgabegerätes verwendet werden – sind fett und kursiv dargestellt. Die obere Hälfte der Tabelle von 00 bis 7F (die Angabe des Codes ist in allen Tabellen hexadezimal) stimmt mit dem ASCII-Zeichensatz überein. ISO 8859-1 wird auch „Latin-1“ genannt und von MS-Windows verwendet (heißt dort aber ANSI-Code: American National Standards Institute) und kann auch auf so gut wie allen Unix-Systemen eingesetzt werden.
Die ISO-8859-Normen werden von ISO/IEC nicht mehr aktiv weiterentwickelt. Für die Zukunft wird eine fortschreitende Ablösung dieser Zeichensätze durch ISO UCS, inhaltsgleich zum Unicode-Standard, erwartet. Dieser findet vor allem in Form der UTF-8-Kodierung immer mehr Verbreitung.
ISO 8859-1 (genauer: ISO/IEC 8859-1) ist ein von der ISO zuletzt 1998 aktualisierter Standard für die Informationstechnik zur Zeichenkodierung mit acht Bit und der erste Teil der Normenfamilie ISO/IEC 8859.
ISO/IEC 8859-1 (siehe Tabelle oben)
| Code | …0 | …1 | …2 | …3 | …4 | …5 | …6 | …7 | …8 | …9 | …A | …B | …C | …D | …E | …F |
| 0… | NUL | SOH | STX | ETX | EOT | ENQ | ACK | BEL | BS | HT | LF | VT | FF | CR | SO | SI |
| 1… | DLE | DC1 | DC2 | DC3 | DC4 | NAK | SYN | ETB | CAN | EM | SUB | ESC | FS | GS | RS | US |
| 2… | SP | ! | „ | # | $ | % | & | ‚ | ( | ) | * | + | , | – | . | / |
| 3… | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | : | ; | < | = | > | ? |
| 4… | @ | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O |
| 5… | P | Q | R | S | T | U | V | W | X | Y | Z | [ | \ | ] | ^ | _ |
| 6… | ` | A | b | c | d | e | f | g | h | i | j | k | l | m | n | o |
| 7… | p | Q | r | s | t | u | v | w | x | y | z | { | | | } | ~ | DEL |
| 8… | PAD | HOP | BPH | NBH | IND | NEL | SSA | ESA | HTS | HTJ | VTS | PLD | PLU | RI | SS2 | SS3 |
| 9… | DCS | PU1 | PU2 | STS | CCH | MW | SPA | EPA | SOS | SGCI | SCI | CSI | ST | OSC | PM | APC |
| A… | NBSP | ¡ | ¢ | £ | ¤ | ¥ | ¦ | § | ¨ | © | ª | « | ¬ | SHY | ® | ¯ |
| B… | ° | ± | ² | ³ | ´ | µ | ¶ | · | ¸ | ¹ | º | » | ¼ | ½ | ¾ | ¿ |
| C… | À | Á | Â | Ã | Ä | Å | Æ | Ç | È | É | Ê | Ë | Ì | Í | Î | Ï |
| D… | Ð | Ñ | Ò | Ó | Ô | Õ | Ö | × | Ø | Ù | Ú | Û | Ü | Ý | Þ | ß |
| E… | à | Á | â | ã | ä | å | æ | ç | è | é | ê | ë | ì | í | î | ï |
| F… | ð | Ñ | ò | ó | ô | õ | ö | ÷ | ø | ù | ú | û | ü | ý | þ | ÿ |
SP (2016, „space“) ist das Leerzeichen, NBSP (A016, „non-breaking space“) das feste Leerzeichen
Windows-1252 (auch: ANSI-Code)
ANSI = American National Standardization Institution.
Deutschsprachige Versionen von Windows (außer DOS-Fenster) verwenden die auf ISO 8859-1 aufbauende Kodierung Windows-1252, vereinfacht auch als ANSI-Code-Tabelle bezeichnet, die sich von den hier angegebenen ASCII-Beispieltabellen relativ stark unterscheidet. 652 Zeichen sind genormt. Ein ASCII-Text mit Umlauten, der unter DOS erstellt wurde, wird also in Windows-Programmen anders erscheinen (die Umlaute werden als Sonderzeichen dargestellt).
Ein Zeichen mit beliebiger Nummer wird so eingegeben: «Alt»-Taste drücken und halten, «0»-Taste auf dem nummerischen Tastenblock eingeben, restliche Nummer auf dem nummerischen Tastenblock eingeben, «Alt»-Taste loslassen.
..│ 0 1 2 3 4 5 6 7 8 9 A B C D E F│/..
──┼────────────────────────────────┼───
20│ ! " # $ % & ' ( ) * + , - . /│032
30│ 0 1 2 3 4 5 6 7 8 9 : ; < = > ?│048
40│ @ A B C D E F G H I J K L M N O│064
50│ P Q R S T U V W X Y Z [ \ ] ^ _│080
60│ ` a b c d e f g h i j k l m n o│096
70│ p q r s t u v w x y z { | } ~ │112
80│ € ' ƒ " . † ‡ ˆ % Š < Œ Ž│128
90│ ' ' " " • – — ˜ T š > œ žŸ│144
A0│ ¡ ¢ £ ¤ ¥ ¦ § ¨ © ª « ¬ - ® ¯│160
B0│ ° ± ² ³ ´ µ ¶ · ¸ ¹ º » ¼ ½ ¾ ¿│176
C0│ À Á Â Ã Ä Å Æ Ç È É Ê Ë Ì Í Î Ï│192
D0│ Ð Ñ Ò Ó Ô Õ Ö × Ø Ù Ú Û Ü Ý Þ ß│208
E0│ à á â ã ä å æ ç è é ê ë ì í î ï│224
F0│ ð ñ ò ó ô õ ö ÷ ø ù ú û ü ý þ ÿ│240
──┼────────────────────────────────┼───
./│ 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1│...
/.│ 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5│...
Aus der linken und der oberen Randspalte kann die hexadezimale, aus der rechten und der unteren Randspalte die dezimale Nummer eines Zeichens abgelesen werden. (Das ‚A‘ hat beispielsweise die Nummer 65.) Damit wird auch die interne Darstellung der Zeichen festgelegt.
UNICODE
Der ASCII-Code mit seinen 128 bzw. 256 Zeichen ist auf Dauer eine unbefriedigende Lösung, da er zum einen nicht allen Alphabeten (etwa kyrillisch, hebräisch, arabisch) gerecht wird, zum anderen durch seine landesspezifischen Erweiterungen die Universalität des Codes aufhebt.
Aus diesem Grund wurde von der ISO („International Standardization Organisation“) ein 32 bit langer Code entwickelt, der Unicode. Er ist in seinem Zeichenvorrat identisch mit ISO 10646; er wird dort als Universal Character Set (UCS) bezeichnet. Der UCS ist ein 32-Code. Er ist in 128 Gruppen aufgeteilt, die hexadezimal von 00 bis 7F durchnummeriert sind. Jede Gruppe besteht ihrerseits aus 256 so genannten „Planes“ (00 bis FF), diese beinhalten letztlich 256 Zeilen mit je 256 Zellen. Von den etwa 4,3 Milliarden darstellbarer Zeichen werden vom UCS jedoch nur die Hälfte verwendet. Ein UCS-Code besteht also aus vier hexadezimalen Zahlen (GGPPRRZZ für Gruppe, Plane, Reihe, Zelle).
Bisher sind ca. 100 000 Zeichen in den Unicode-Standard aufgenommen worden (Stand: 2008).
Bereits jetzt wurden festgelegt: ASCII, Latin-1 (= ANSI), griechische, kyrillische, armenische, hebräische, südostasiatische Zeichen sowie diverse mathematische Symbole und geometrische Formen.
UTF-8
UTF-8 (Abk. für 8-bit Unicode Transformation Format) ist die am weitesten verbreitete Kodierung für Unicode-Zeichen. UTF-8 ist eine 8-Bit-Kodierung von Unicode, die zu ASCII abwärtskompatibel ist
Dabei wird jedem Unicode-Zeichen eine speziell kodierte Bytekette von variabler Länge zugeordnet. UTF-8 unterstützt bis zu vier Byte, auf die sich wie bei allen UTF-Formaten alle Unicode-Zeichen abbilden lassen.
UTF-8 hat eine zentrale Bedeutung als globale Zeichenkodierung im Internet. Die Internet Engineering Task Force verlangt von allen neuen Internetkommunikationsprotokollen, dass die Zeichenkodierung deklariert wird und dass UTF-8 eine der unterstützten Kodierungen ist. Das Internet Mail Consortium (IMC) empfiehlt, dass alle E-Mail-Programme UTF-8 darstellen und senden können. 2008 wird diese Empfehlung allerdings immer noch nicht global befolgt.
In HTML 5 ist eine allgemeine Codekennzeichnung in folgender Form vorgesehen:
<meta charset="utf-8">
Im März 2019 verwendeten etwa 93,1 % aller Websites diese Codierung.
Die Einbindung von Unicode-Zeichen in Websites kann so erfolgen:
<p>Ein Pique-Zeichen: ♠</p> dezimaler Unicode-Wert
<p>Ein Pique-Zeichen: ♠</p> hexadezimaler Unicode-Wert
Escape-Sequenzen: Die ersten 32 ASCII-Zeichen stehen für Steuerzeichen. Diese werden verwendet, um Geräte zu steuern, etwa Drucker oder Bildschirmterminals. Da in der Programmierung diese Zeichen nicht eingegeben werden können, behilft man sich mit der Kombination eines „Umschaltzeichens“ und eines normalen Zeichens. Ursprünglich wurde als Umschaltzeichen ESC (ASCII dezimal 27, hexadezimal 1B) verwendet.
In C/C++ und ähnlichen Programmiersprachen (Java, Javascript, Python, …) hat sich (statt des ESC-Zeichens) der Backslash \ etabliert. Beispiele:
\c Zeilenumbruch
\t horizontaler Tabulator
\" Anführungszeichen (dieses würde normalerweise eine Zeichenkette begrenzen)
\x40 ASCII-Zeichen mit der hexadezimalen Nummer 40 (also @)
\u20ac Unicode-Zeichen mit der hexadezimalen Nummer 20AC (also €)
JavaScript-Beispiel:
var str="Ein großes Omega sieht wie folgt aus: \u03A9"
EBCDI-Code
Dieser Code wird überwiegend in Großrechenanlagen (etwa von IBM, Unisys) verwendet. Der Extended Binary Coded Decimal Interchange Code kann für die Codierung von Zahlen, Buchstaben und Sonderzeichen verwendet werden. Dieser Code ist ein 8-bit-Code, das heißt, jedem alphanumerischen Zeichen wird eine 8-stellige Binärzahl zugeordnet, zum Beispiel
A ... 1100 0001 (dezimal 193)
Codierungssysteme in der Industrie
Strich- oder Balkencode
Fast alle Waren tragen heute einen Strichcode, der die 13-stellige Europäische Artikel-Nummer (EAN) enthält. Die EAN verschlüsselt das Herstellungsland, den Herstellungsbetrieb und die Artikelnummer eines jeden Produkts.
Von links nach rechts gelesen bedeuten:

2 Stellen das Länderkennzeichen (90, 91 = Österreich)
5 Stellen die bundeseinheitliche Betriebsnummer
5 Stellen die Artikelnummer des Herstellers
1 Stelle die Prüfziffer
Transpondersysteme
In den letzten Jahren entwickelten sich Transpondersysteme in allen Kontrollbereichen der Industrie und der Privatwirtschaft zu einer echten Alternative. So ersetzen diese Systeme heutzutage in immer größerem Umfang die konventionellen Lösungen zur Zugangskontrolle, Zeiterfassung, Kontrolle von Materialbewegungen u.v.m.. Transpondersysteme zeichnen sich in allen diesen Bereichen durch Robustheit, Flexibilität und problemlose Erweiterbarkeit aus.
Der Transponder selbst besteht im Wesentlichen aus einer Spule und einem elektronischen Bauteil, dem eine einmalige Seriennummer „eingebrannt“ ist. Des weiteren sind Transponder, angepasst auf entsprechende Einsatzanforderungen, in vielen Bauformen lieferbar.
Im Aufbau unterscheiden sich die verschiedenen Transpondersysteme zwar in bestimmten Details, die Hauptkomponenten und die Funktionsweise können jedoch systematisch und systemübergreifend dargestellt werden.
So umfasst eine minimale Transponderanwendung nur eine Lesestation, die beim Erkennen eines gültigen Transponders eine Funktion auslöst. Wird nun ein Transponder in die Nähe der Lesestation gebracht, so wird er von der Lesestation über die Spule berührungslos mit Strom versorgt und sendet seine Seriennummer zur Lesestation.
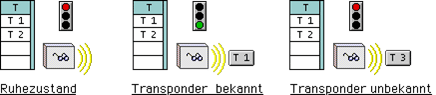
Stehen mehrere Lesestationen mit einem System in Verbindung kann mit einer Zentraleinheit festgestellt werden, ob mit diesem Transponder eine Funktion ausgeführt wird oder nicht.

Aus diesem Verhalten von Transpondersystemen ergeben sich grundsätzliche Vorteile zu konventionellen Lösungen:
Jeder Transponder ist ein Unikat, es existieren keine Kopien (Nachschlüssel).
Bei einer mechanischen Schließanlage sind alle oder viele Schlüssel für ein Schloss gleich. Geht ein Schlüssel verloren, so müssen alle Schlüssel und alle Schlösser ausgetauscht werden. Das gleiche gilt, wenn einem Benutzer die Zugangsberechtigung entzogen werden soll und dieser den Schlüssel nicht zurückgibt. Der Austausch kann, je nach Umfang der Schließanlage, natürlich sehr teuer werden. Bei einem Transpondersystem muss nur die Berechtigung des einzelnen Benutzers (Transponders) gelöscht oder ersetzt werden.
Da Datenübertragung und Stromversorgung berührungslos erfolgen, sind Transpondersysteme, besonders vandalen- und betriebssicher. Sie können in Bereichen mit hohem Schmutzaufkommen oder Hygieneanforderungen eingesetzt werden. Es entstehen auch keine Probleme mit leeren Batterien in Handsendern, Tastaturen die ausgespäht, Schlüssellöcher die verklebt, Kartenschlitze die verstopft und Kontakte die verschlissen werden können.
In vielen Zentraleinheiten kommt ein Kleincomputer, ein sogenannter Mikrocontroller, zum Einsatz (Embedded System). Somit können alle weiteren Vorteile der elektronischen Datenverarbeitung genutzt werden. Beispielsweise kann die Zugangsberechtigung an bestimmte Uhrzeiten gebunden oder eingeschränkt werden (z.B. nur noch Verlassen des Objekts, jedoch nicht betreten).
Es können zusätzliche kundenspezifische Funktionen programmiert werden, z.B. Zeiterfassung, Zählfunktionen, Anwesenheitslisten, Benutzerprotokolle, Alarmierung o.ä.
Oft kann zusätzlich zu einem (Erst-)Transponder auch ein Reservetransponder verwendet werden. Dies ist jedoch nicht mit einem „Zweitschlüssel“ in einer Schließanlage zu vergleichen. Während ein Zweitschlüssel wie der Erstschlüssel benutzt werden kann, sperrt die erstmalige Verwendung des Reservetransponders automatisch den Ersttransponder. Ist dieser verloren gegangen, so kann sich der Finder nach der ersten Verwendung des Reservetransponders keinen unbefugten Zugang mehr verschaffen.
RFID (Radio Frequency Identification)
Dabei handelt es sich um Chips (Speicherkapazität 96 bit), die ohne eigene Stromversorgung in einem niederfrequenten Feld eine Kennung (etwa die Europäische Artikelnummer) aussenden, um Gegenstände zu identifizieren. Um einen internationalen Einsatz zu ermöglichen, müssen sich die Hersteller allerdings noch auf einheitliche Frequenzen einigen. Ein möglicher Frequenzbereich liegt bei 860 – 930 MHz (Ultrakurzwellen-Bereich). Es gibt bereits Chips, die nicht aus Silicium, sondern aus organischen Kunststoffmaterialien hergestellt werden und so in Strichcodeetiketten integriert werden können.
Eine weitere Anwendung ist bereits beschlossen: Europäische Reisepässe werden künftig einen Speicherchip mit digitalisiertem Foto und Fingerabdrücken enthalten. Sobald die technischen Einzelheiten festgelegt sind, haben die EU-Staaten 18 Monate Zeit, um die digitalisierten Passbilder einzuführen. Weitere 18 Monate bleiben ihnen dann noch, um auch die Fingerabdrücke in den Pass aufzunehmen.
Fehlerkorrektur von Codes
Ein ganz wichtiges Problem in der Informatik ist die Fehlerkorrektur von Codes. Schon innerhalb des Rechners werden laufend Daten übertragen. Was ist, wenn nun Fehler auftreten? Ist der Computer in der Lage, Fehler zu erkennen und nötigenfalls zu beheben?
Dazu betrachten wir zwei BCD-Ziffern:
610 = 0110
710 = 0111
Wir sehen: In diesem Fall gibt es ein unterschiedliches Bit. (Man sagt: Die Hamming-Distanz beträgt 1.) Wenn statt 0 im letzten Bit 1 übertragen wird, entsteht ein Fehler!
Man muss also gewährleisten, dass die Hamming-Distanz zwischen zwei beliebigen Ziffern immer mindestens 2 ist.
Hier gibt es mehrere Methoden.
Beispiel: Parity Check (Paritätsprüfung)
Man führt ein Prüfbit – also ein 5. Bit zur Kontrolle – ein. Bei gerader Parität („even parity“) ist die Quersumme eine gerade Zahl, bei ungerader Parität („odd parity“) ist die Quersumme ungerade. Das 5. Bit muss dementsprechend gewählt werden.
Also gilt für even parity:
010 = 00000
110 = 00011
210 = 00101
310 = 00110
410 = 01001
510 = 01010
610 = 01100
710 = 01111
810 = 10001
910 = 10010
(In der odd parity-Tabelle steht statt 0 1, und statt 1 findet man 0.)
Dieses Prüfbit ist eine Information, die eigentlich nicht mehr notwendig ist. Die Angabe solcher an sich nicht notwendigen Zusatzinformationen bezeichnet man als Redundanz. Redundante Codes können also Übertragungsfehler aufzeigen.
Sollen Fehler, die bei der Übertragung eines Zeichens entstanden sind, nicht nur erkannt, sondern auch korrigiert werden können, so muss die Redundanz des Codes weiter erhöht werden. Am einfachsten ist dies möglich, wenn man fehlererkennbare Zeichen überträgt, die vom Empfänger überprüft werden. Stellt der Empfänger einen Fehler fest, so fordert er den Sender zur Wiederholung des Zeichens auf. Um die Redundanz nicht allzu sehr zu vergrößern, fasst man häufig mehrere Zeichen zu einem Block zusammen, welcher als Ganzes empfangsseitig überprüft wird.
Beispiel: Blockcodes
Man ordnet die zu überprüfenden Daten in einen (zum Beispiel quadratischen) Raster ein und berechnet für jede Spalte und jede Zeile ein Prüfbit (etwa wie oben aus der Quersumme – etwa gerade Quersumme 0, ungerade 1). Diese Prüfbits werden mit übertragen:
Prüfbit 1. Info 0 1 0 1 1 0 1 1 1 2. Info 1 0 0 0 1 0 0 0 0 3. Info 0 0 0 1 1 1 0 1 0 4. Info 1 1 0 1 0 0 0 1 0 5. Info 0 0 0 0 0 0 0 0 0 6. Info 0 0 1 1 1 0 1 1 1 7. Info 1 0 0 0 1 0 0 1 1 8. Info 1 1 1 0 0 0 1 0 0 Prüfbit 0 1 0 0 1 1 1 1
Tritt ein Übertragungsfehler auf, so kann man aufgrund der Prüfbits genau feststellen, in welcher Reihe und in welcher Spalte der Fehler aufgetreten ist, d.h. der Fehler kann festgestellt und korrigiert werden. Bei zwei Übertragungsfehlern ist keine Korrektur mehr möglich.
Mit diesem Blockcode ist es also möglich, mit n Prüfbits (im angegeben Beispiel 16 bit) eine Sicherung von n2/4 Datenbits (im angegebenen Beispiel 64) zu erreichen.
Es gibt andere Verfahren, die mit weniger Redundanz auskommen (Beispiel: Hamming-Code u.a.).
Je größer die Hamming-Distanz, desto größer wird die Sicherheit. Bei Hamming-Distanz 2 ist 1 Fehler erkennbar, bei 3 ist 1 Fehler korrigierbar, bei 4 sind 2 Fehler erkennbar usw.
Beispiel: CRC (Cyclic Redundancy Check): Wird sehr häufig verwendet, etwa bei der Fehlerkorrektur von Festplatten und für die Überprüfung bei Datenübertragungen, aber auch beim Testen der Arbeitsspeichermodule beim Hochfahren des PCs. Der CRC basiert mathematisch gesehen auf Polynomdivisionen.
Speicherung von audiovisuellen Daten
Als Analogsignal wird ein Signal bezeichnet, wenn seine Stärke (Amplitude) kontinuierlich jeden Wert zwischen einem Minimum und einem Maximum annehmen kann. Dieses trifft auf nahezu alle realen Prozesse oder Zustände zu. Theoretisch ist es möglich, beliebig kleine Signaländerungen zu registrieren.
Üblicherweise versteht man unter Analogsignal ein elektrisches Signal, meistens die elektrische Spannung, seltener Frequenz, Stromstärke oder Ladung. Man kennt aber auch analoge Signale auch aus mechanischen, pneumatischen, hydraulischen und anderen Systemen.
Der Hauptnachteil analoger Signale sind zufällige Variationen, die zwangsläufig auftreten, da kein System störungsfrei ist, und die im Gegensatz zu digitalen Signalen nicht mit Hilfe von Prüfbits korrigiert werden können. Hierbei gilt: je häufiger ein Signal kopiert wird oder je länger der Signalweg, desto stärker wird das Signal vom Rauschen dominiert. Diese Signalverluste und Signalverzerrungen sind unumkehrbar, da eine Verstärkung des Signals zusätzliches Rauschen addiert.
Ein Digitalsignal (von lat. digitus = Finger; mit Fingern wird gezählt!) überträgt eine Information, zum Beispiel eine elektrische Wechselspannung, in Form einer Zahlenkolonne, die die Information mathematisch beschreibt, im Gegensatz zum Analogsignal, das eine physikalische Größe entweder direkt überträgt oder durch eine andere physikalische Größe abbildet.
Zur Umwandlung in ein Digitalsignal muss das analoge Ausgangssignal zunächst zeitlich quantisiert werden, das heißt in feste Zeit-Intervalle zerlegt. Beispiel: bei der Aufnahme einer Audio-CD wird jeder Kanal (links/rechts) des Ausgangssignals 44.100-mal pro Sekunde abgetastet. Diese Frequenz von 44,1 kHz bezeichnet man als Samplingfrequenz oder Abtastrate. Details des Ausgangssignals, die feiner sind als dieses Zeitraster, können nicht erfasst werden.
Nyquist-Shannon-Abtasttheorem (in neuerer Literatur auch WKS-Sampling-Theorem genannt; WKS steht für Whittaker-Kotelnikow-Shannon): Das Abtasttheorem besagt, dass ein kontinuierliches, bandbegrenztes Signal, mit einer Minimalfrequenz von 0 Hz und einer Maximalfrequenz fmax, mit einer Frequenz größer als 2 · fmax abgetastet werden muss, damit man aus dem so erhaltenen zeitdiskreten Signal das Ursprungssignal ohne Informationsverlust exakt rekonstruieren und beliebig genau approximieren kann.
Speicherung von Grafikdaten
Verlustfreie Kompressionsverfahren
GIF (Graphics Interchange Format; engl. Grafikaustausch-Format) ist ein Grafikformat mit guter verlustfreier Komprimierung für Bilder mit geringer Farbtiefe (bis zu 256 verschiedene Farben pro Einzelbild). Darüber hinaus können mehrere Einzelbilder in einer Datei abgespeichert werden, die von Webbrowsern als Animationen interpretiert werden.
Die erste 1987 herausgebrachte GIF-Version war die Version „87a“. Im Jahr 1989 veröffentlichte CompuServe eine erweiterte Version, die „89a“ genannt wird. Man kann die Version an den ersten sechs Bytes einer GIF-Datei erkennen, der sogenannten Signatur. Interpretiert man diese als ASCII-Zeichen, so steht dort GIF87a bzw. GIF89a.
Bei GIF sind die Farbinformationen in einer Farbtabelle abgelegt. Diese kann bis zu 256 verschiedene Einträge enthalten, die frei aus 2563 ~ 16,7 Millionen möglichen Farbwerten auswählbar sind.
Ab GIF89a kann ein Farbeintrag in der Palette als transparent definiert werden. Dadurch kann man an beliebigen Stellen die jeweilige Hintergrundfarbe durchscheinen lassen und den Eindruck erwecken, ein GIF-Bild hätte eine nicht rechteckige Form.
Häufig wird zur Datenkompression der Lempel-Ziv-Welch-Algorithmus (LZW) benutzt.
Verlustbehaftete Kompressionsverfahren
JPEG ist die gebräuchliche Bezeichnung für die 1992 vorgestellte Norm ISO/IEC 10918-1 bzw. CCITT Recommendation T.81, die verschiedene Methoden der Bildkompression beschreibt. Die Bezeichnung „JPEG“ geht auf das Gremium Joint Photographic Experts Group zurück, das die JPEG-Norm entwickelt hat.
Die Kompression erfolgt durch das Anwenden mehrerer Verarbeitungsschritte, von denen nur zwei verlustbehaftet sind.
- Farbraumumrechnung vom (meist) RGB-Farbraum ins YCbCr-Farbmodell (nach IEC 601).
- Tiefpassfilterung und Unterabtastung der Farbabweichungssignale Cb und Cr (verlustbehaftet).
- Einteilung in 8×8-Blöcke und diskrete Kosinustransformation dieser Blöcke.
- Quantisierung (verlustbehaftet).
- Umsortierung.
- Entropiekodierung
Speicherung von Audiodaten
Audio-Rohmaterial benötigt viel Speicherplatz (1 Minute Stereo in CD-Qualität benötigt etwa 10 MB) und zum Transfer (beispielsweise über das Internet) hohe Datenübertragungsraten und/oder viel Zeit. Die verlustlose Komprimierung reduziert die zu übertragenden Datenmengen nicht so stark wie verlustbehaftete Verfahren, die für die meisten Fälle (Ausnahmen sind beispielsweise Studioanwendungen oder Archivierung) noch annehmbare Qualität liefern. So erlangte das MP3-Format für Audio-Daten schnell den Status, den die JPEG-Komprimierung für Bilddaten hat.
MP3 (MPEG-1 Audio Layer 3) ist ein Dateiformat zur verlustbehafteten Audiodatenkompression. MP3 bedient sich dabei der Psychoakustik mit dem Ziel, nur für den Menschen bewusst hörbare Audiosignale zu speichern. Dadurch wird eine Datenkompression möglich, welche die Audioqualität nicht oder nur gering beeinträchtigt. Das Format ist ein indirekter Vorgänger qualitativ und funktionell überlegener Formate wie AAC oder Vorbis.
Wie die meisten verlustbehafteten Kompressionsformate für Musik nutzt MP3 sogenannte psychoakustische Effekte der Wahrnehmung aus. Zum Beispiel kann der Mensch zwei Töne erst ab einem gewissen Mindestunterschied der Tonhöhe (Frequenz) voneinander unterscheiden, und er kann vor und nach sehr lauten Geräuschen für kurze Zeit leisere Geräusche schlechter oder gar nicht wahrnehmen. Man braucht also nicht das Ursprungssignal exakt abzuspeichern, sondern es reichen die Signalanteile, die das menschliche Gehör auch wahrnehmen kann. Die Aufgabe des Kodierers ist es, das Signal so aufzuarbeiten, dass es weniger Speicherplatz benötigt, aber für das menschliche Gehör noch genauso klingt wie das Original.
Der Dekoder erzeugt aus diesen MP3-Daten dann ein für die überwiegende Anzahl von Hörern original klingendes Signal, das aber nicht mit dem Ursprungssignal identisch ist, da bei der Umwandlung in das MP3-Format Informationen entfernt wurden.
Advanced Audio Coding (AAC) ist ein im Rahmen von MPEG-2 und MPEG-4 standardisiertes Verfahren, welches von mehreren großen Firmen entwickelt wurde. Apple und Real Media setzen dieses Format für ihre Online-Musikläden ein, und die Nero AG stellt einen Encoder für das Format bereit. Mit faac ist auch ein freier Encoder erhältlich.[9] AAC ist bei niedrigen Bitraten bis etwa 160 kbit/s MP3 in der Klangqualität überlegen – je niedriger die Bitrate, desto deutlicher –, erlaubt Mehrkanal-Ton, und wird von der Industrie (z. B. bei Mobiltelefonen und MP3-Playern) breit unterstützt.
MIDI (engl.: musical instrument digital interface = „Digitale Schnittstelle für Musikinstrumente“) ist ein Datenübertragungs-Protokoll zum Zwecke der Übermittlung, Aufzeichnung und Wiedergabe von musikalischen Steuerinformationen zwischen Instrumenten oder mit einem PC. Das MIDI-Protokoll wird von vielen Instrumenten und Soundkarten in modernen Rechnern unterstützt.
Studium an der TU Wien (Chemie, Physik, Mathematik, Informatik), selbstständige Tätigkeit (IT & Consulting) mit Spezialisierung auf Schulungskonzepte in der Erwachsenenbildung, derzeit Unterrichtstätigkeit am Francisco Josephinum Wieselburg (Landtechnik-Abteilung, technische und naturwissenschaftliche Fächer, Schwerpunkte Elektro- und Automatisierungstechnik und Mechanik), seit unendlich langer Zeit dem ClubComputer freundschaftlich verbunden, Autor von Artikeln in PCNEWS.



Neueste Kommentare