Digitaltechnik „begreifbar machen“

Digitaltechnik „begreifbar machen“

Die Digitaltechnik befasst sich mit digitalen Schaltungen. Diese Schaltungen bestimmen den Aufbau und die Funktionsweise nahezu aller heute verwendeten informationsverarbeitenden Systeme. Die zunehmende Nutzung dieser Systeme wird allgemein als Digitalisierung bezeichnet. Die Digitaltechnik bildet somit die Grundlage für das, was unser Leben und unsere Welt in den letzten Jahrzehnten tiefgreifend verändert hat und zukünftig wohl noch mehr bestimmen wird.

Eine zeitgemäße und zukunftsorientierte schulische Ausbildung sollte dieser Entwicklung Rechnung tragen, auch im allgemeinbildenden Bereich. Das sollte aber nicht nur über einen medienpädagogischen Ansatz erfolgen, bei dem digitale Systeme mehr oder weniger „als Blackbox“ betrachtet werden und es vor allem um deren kompetente und kritische Nutzung geht. Um das „Wesen der Digitalisierung“ wirklich begreifen zu können, ist auch eine Auseinandersetzung mit grundlegenden Konzepten und Inhalten der Informatik und Digitaltechnik erforderlich. Dabei geht es beispielsweise um Fragen wie „Was bedeutet eigentlich digital?“, „Wie können digitale Systeme rechnen?“ oder „Wie können digitale Systeme Informationen speichern?“. Eine Allgemeinbildung einer Informationsgesellschaft im Informationszeitalter sollte das Wissen vermitteln, um diese Fragen beantworten zu können.

In diesem Beitrag wird ein methodisches und didaktisches Konzept zur Vermittlung von Digitaltechnik kursorisch vorgestellt. Es wird vom Autor schon mehrere Jahre lang an einer AHS mit Informatik-Schwerpunkt in der 10. und 11. Schulstufe eingesetzt. Das Konzept verfolgt vor allem das Ziel, den Unterricht möglichst anschaulich und aktiv zu gestalten. Einfache digitale Schaltungen werden beispielsweise auf Steckbrettern in „Maker- Manier“ aufgebaut und sind damit „angreifbar und besser begreifbar“. Für die Erstellung komplizierterer Schaltungen werden einige sehr einfach und intuitiv zu bedienende grafische Simulationstools wie Logicly und Tinkercad-Circuits eingesetzt. Es werden auch FPGA-Boards genutzt, um Schaltungen auf Microchip-Ebene zu implementieren.

Das Herzstück vieler digitaler Systeme stellen Mikroprozessoren dar. Diese gehören wohl zu den kompliziertesten Objekten, welche die Menschheit je geschaffen hat. Moderne Prozessoren können mehrere Milliarden Transistoren enthalten, welche über kilometerlange Leiterbahnen zu digitalen Schaltungen miteinander verbunden sind. Diese befinden sich in einem Silizium-Plättchen, das nicht viel größer ist, wie ein Daumennagel. Dies lässt vermuten, dass nur mit einem entsprechenden Expertenwissen der Aufbau und die Funktionsweise dieser Systeme verstanden werden kann. Bei genauerer Betrachtung stellt sich aber heraus, dass dies in Grundzügen durchaus auch ohne spezielles Knowhow möglich ist. Der Schlüssel dazu ist das Prinzip der Abstraktion.

Laut Wikipedia bezeichnet Abstraktion „den induktiven Denkprozess des erforderlichen Weglassens von Einzelheiten und des Überführens auf etwas Allgemeineres oder Einfacheres.“ Diese besondere Fähigkeit des menschlichen Denkens sorgt einerseits dafür, dass wir uns in der Komplexität der uns umgebenden Welt zurechtfinden können, indem wir nur das jeweils Wesentliche beachten. Andererseits verschafft sie uns auch die Möglichkeit, komplizierte Systeme in strukturierter Art und Weise zu erzeugen. Abstraktionen werden dabei Schicht für Schicht aufgebaut, was zu immer höheren Ebenen und Fähigkeiten führt. In der Digitaltechnik wird das besonders augenscheinlich: Funktioniert eine digitale Schaltung wie erwartet, kann sie als neue funktionale Einheit – als integrierter Schaltkreis (IC) – für die Entwicklung komplizierterer Schaltungen verwendet werden. Ihr konkreter interner Aufbau ist bei dieser Verwendung nicht mehr von Bedeutung. Die Abstraktion ermöglicht dabei eine zunehmende Kompliziertheit der Schaltungen und sorgt dafür, dass diese auch beherrschbar bleibt.

Dieses Prinzip lässt sich auch in didaktischer Hinsicht sehr gut nutzen, um schrittweise ein Verständnis über den Aufbau und die Funktionsweise digitaler Schaltungen zu vermitteln (vom Einfachen zum Komplizierten). Die Digitaltechnik als Wissenschaft gibt dabei den Weg theoretisch vor. Wenn dieser Weg mit entsprechenden Praxisbeispielen anschaulich und aktiv gestaltet wird, sind die Lernenden dabei auch entsprechend motiviert und erleben dann das Entdecken und Verstehen dieser Zusammenhänge oftmals sogar als persönlichen Erfolg.

Das vorgestellte Unterrichtskonzept eignet sich nach Meinung des Autors sehr gut für den Wahlpflichtgegenstand Informatik in der AHS-Oberstufe. Teile davon lassen sich auch in den Unterricht im Informatik-Pflichtgegenstand integrieren. Die praktische Umsetzbarkeit der vorgestellten digitalen Schaltungen ist unterschiedlich, was Schwierigkeit und Zeitaufwand betrifft.  Bei einer entsprechenden Ausstattung und Vorbereitung können alle Schaltungen von den Schülerinnen und Schülern selbst aufgebaut werden. Je nach Schwerpunktsetzung und verfügbarer Unterrichtszeit kann es auch sinnvoll sein, bereits vorgefertigte Schaltungen zum Testen und Experimentieren bereit zu stellen oder deren Schaltverhalten nur zu demonstrieren und zu erörtern.

Im Folgenden wird beschrieben, wie Schaltungen mit Feldeffekttransistoren, wie Logikgatter, Arithmetik-Schaltungen, eine ALU, einfache Speicherbausteine (Latches, Flipflops und Register) und eine Zählerschaltung unter Anwendung der erwähnten didaktischen und methodischen Hilfsmittel Schritt für Schritt und aufeinander aufbauend erstellt werden können. Damit sollen grundlegende Einsichten und Kenntnisse über den Aufbau und die Funktionsweise von Computersystemen im Allgemeinen und von Mikroprozessoren im Speziellen vermittelt werden.

Ein Verständnis der binären Digitaltechnik setzt ein Verständnis der binären Informationsdarstellung voraus. Das gilt es aus didaktischer Sicht zu berücksichtigen. Theoretische Kenntnisse über das binäre Zahlensystem, die Zweierkomplement-Darstellung, das Rechnen mit binären Zahlen und Grundlagen der Booleschen Algebra sollten entweder vorweg oder begleitend vermittelt werden.

Die Basis: Feldeffekttransistoren

Die kleinsten funktionalen Einheiten von Mikroprozessoren sind Feldeffekttransistoren (FETs). Moderne CPUs enthalten mehrere Milliarden davon. Sie sind miteinander elektrisch leitend verbunden und fungieren als winzige Ein- und Ausschalter. Besonders bemerkenswert sind ihre Kleinheit und ihr Schaltverhalten. Ihre Abmessungen bewegen sich in der Größenordnung von 100 Nanometern und sie können mehrere Milliarden mal pro Sekunde aus- und eingeschaltet werden.

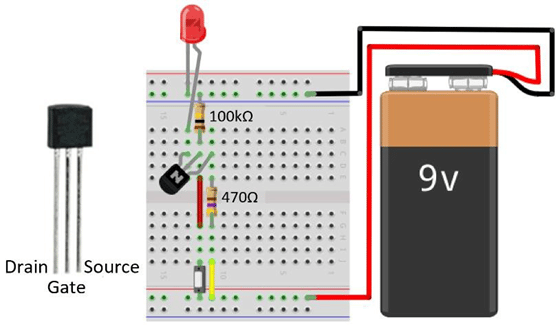
Der MOSFET BS170 (vgl. https://onsemi.com/ pdf/datasheet/mmbf170-d.pdf) ist ein solcher Feldeffekttransistor, genauer ein Metall-Oxid-Halbleiter-Feldeffekt-Transistor (Metal-Oxide-Semiconductor Field-Effect-Transistor). Seine Abmessungen sind verglichen mit den FETs in einer CPU „gigantisch“. Dadurch kann er aber „angefasst werden“ und eignet sich zum Aufbau von Schaltungen auf Steckbrettern (vgl. Abb.1). Er wird über eine elektrische Spannung und ein dadurch erzeugtes elektrisches Feld am Gate-Anschluss gesteuert. Mit diesem kann der Stromfluss zwischen Source und Drain aus- und eingeschaltet werden. Dies lässt sich mit der in Abb.1 dargestellten Schaltung genauer untersuchen.

Wird der 9V-Block angeschlossen und der Taster betätigt, leuchtet die LED auf. Sie erlischt sofort, wenn der Taster losgelassen wird. Das Drücken des Tasters bewirkt, dass am mittleren Anschluss des Transistors, dem Gate, über die rote Steckbrücke hinweg eine elektrische Spannung angelegt und dadurch der Transistor durchgeschalten wird. Es kann nun ein elektrischer Strom zwischen dem Plus-Pol und dem Minus-Pol der Batterie fließen. Der Stromfluss erfolgt dabei über die gelbe Steckbrücke, den 470Ω-Widerstand, durch den Transistor (zwischen Source und Drain) und über die LED, welche dadurch aufleuchtet. Der Widerstand von 100kΩ am Gate-Anschluss ist notwendig, damit von dort nach dem Ausschalten überschüssige Ladung sofort abfließen kann.

Das Schaltverhalten der Feldeffekttransistoren in Mikroprozessoren wird also durch den Spannungspegel am Gate-Anschluss bestimmt. Es werden dabei nur zwei Zustände unterschieden: Hoher Spannungspegel (High, An, 1) und niedriger Spannungspegel (Low, Aus, 0). Die damit aufgebauten elektronischen Schaltungen werden daher als binäre Schaltungen bezeichnet.

Allgemein werden in der Elektronik digitale und analoge Signale unterschieden. Charakteristisch für analoge Signale ist ihr kontinuierlicher Wertebereich. Im Gegensatz dazu besitzen digitale Signale nur eine endliche Zahl diskreter Werte. Die Digitaltechnik befasst sich mit solchen Signalen. Sind es – so wie bei den Feldeffekttransistoren in den Mikroprozessoren – nur zwei diskrete Werte, spricht man auch von der binären Digitaltechnik.

Die nächste Ebene: Logik-Gatter

Die Feldeffekttransistoren in Mikroprozessoren sind miteinander elektrisch leitend verbunden, um elektronische Schaltungen zu bilden. Auf der nächsten Abstraktionsebene sind dies zunächst Logik-Gatter wie z.B. AND, OR, XOR, NAND, NOR, XNOR und NOT.

Die beiden Logik-Gatter OR und AND lassen sich beispielsweise mit jeweils zwei MOSFETs auf einem Steckbrett, wie in Abb.2 gezeigt, als einfache Parallel- und Reihenschaltung aufbauen.

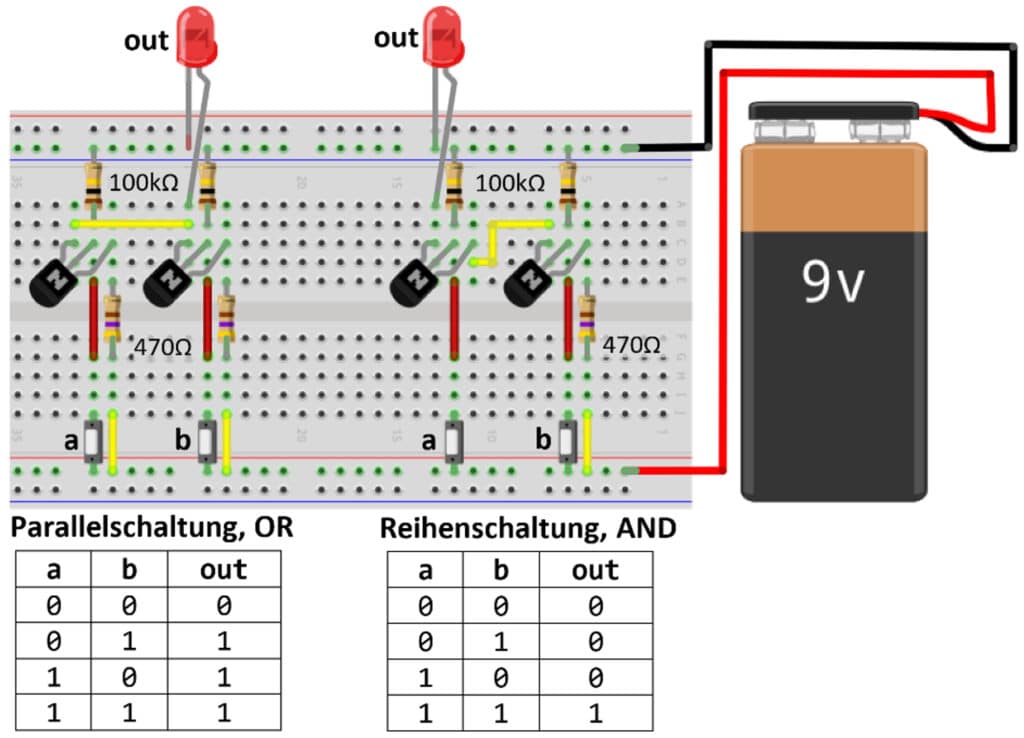
Das Online-Tool Tinkercad-Circuits (https://www.tinkercad.com/circuits) ermöglicht die virtuelle Erstellung von Schaltungen in einem Browser. Es wird eine Vielzahl elektronischer Bauteile zur Verfügung gestellt, die auf virtuellen Steckbrettern sehr einfach platziert und miteinander verbunden werden können. Im Simulationsmodus kann dann das Verhalten der Schaltung beobachtet und getestet werden.

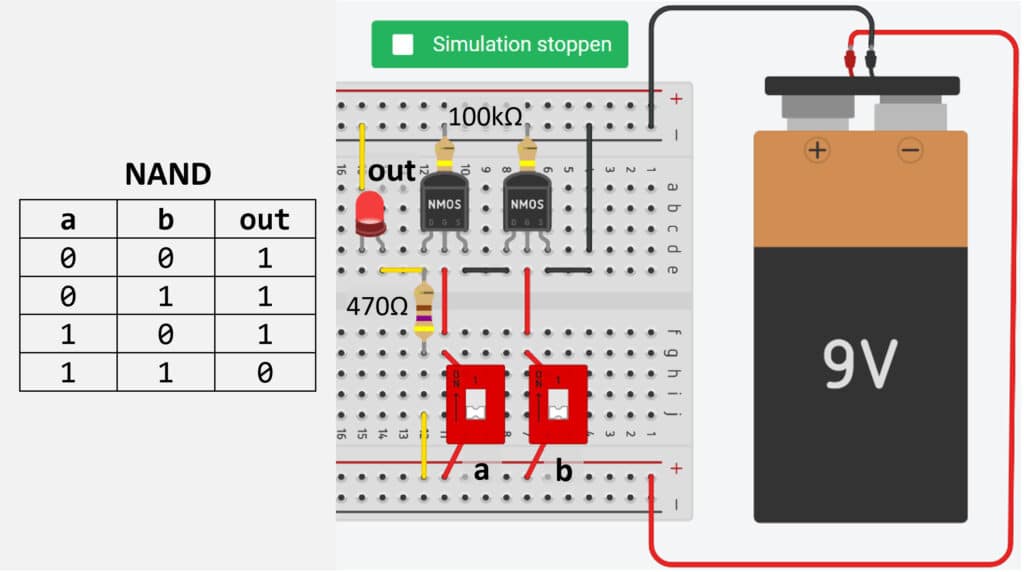
Abb.3 zeigt ein mit Tinkercad-Circuits aus zwei FETs erstelltes NAND-Gatter. Die schaltungstechnische Realisierung erfolgt dabei mit zwei in Reihe geschalteten FETs (NMOS- Bausteinen), die out auf Masse (logisch 0, schwarze Leiterbahnen) legen, wenn beide durchgeschalten sind und der Strom aufgrund des geringeren Widerstands durch sie hindurchfließt und nicht durch die LED. Ist ein FET oder sind beide FETs nicht durchgeschalten, so ist die Masseverbindung unterbrochen. Der Strom fließt dann durch die LED und bringt diese zum Aufleuchten (logisch 1, gelbe Leiterbahn). Vor der LED befindet sich ein 470Ω-Widerstand, hinter den FETs jeweils ein 100kΩ-Widerstand. Die in Abb.3 enthaltene Wahrheitstabelle kann mit der Simulationsfunktion von Tinkercad-Circuits ermittelt werden.

NAND als Universalgatter

Die beiden Logik-Gatter NAND und NOR zeichnen sich dadurch aus, dass mit ihnen jeweils alle anderen Logikgatter (AND, OR, XOR, XNOR, NOT und NOR bzw. NAND) aufgebaut werden können. Vor allem NAND-Gatter gelten daher in der Digitaltechnik als Standardbausteine.

So enthält z.B. der CD4011BE (vgl. https://www.ti.com/lit/ds/symlink/cd4011b.pdf) als integrierter Schaltkreis vier NAND-Gatter. Er gehört zur CMOS-Familie 4000 (CMOS: Complementary Metal-Oxide-Semiconductor). ICs dieser Familie können mit Betriebsspannungen zwischen 3 und 18V betrieben werden. Damit eignen sie sich sehr gut für einfache Experimente mit einer 9V-Batterie als Spannungs- und Stromquelle. Der CD4011BE besitzt 14 Pins (vgl. Abb.4). Er benötigt zum Betrieb eine Versorgungsspannung, welche zwischen Pin 14 (Vdd, +Pol) und Pin 7 (Vss, -Pol) angelegt werden muss. Die übrigen 12 Anschlüsse gehören zu seinen vier NAND-Gattern. Nicht verwendete Eingänge müssen beim Betrieb entweder auf das Potential von Vss oder Vdd gelegt werden, da sie sonst zu einer Fehlfunktion führen. Offene Ausgänge sind hingegen erlaubt.

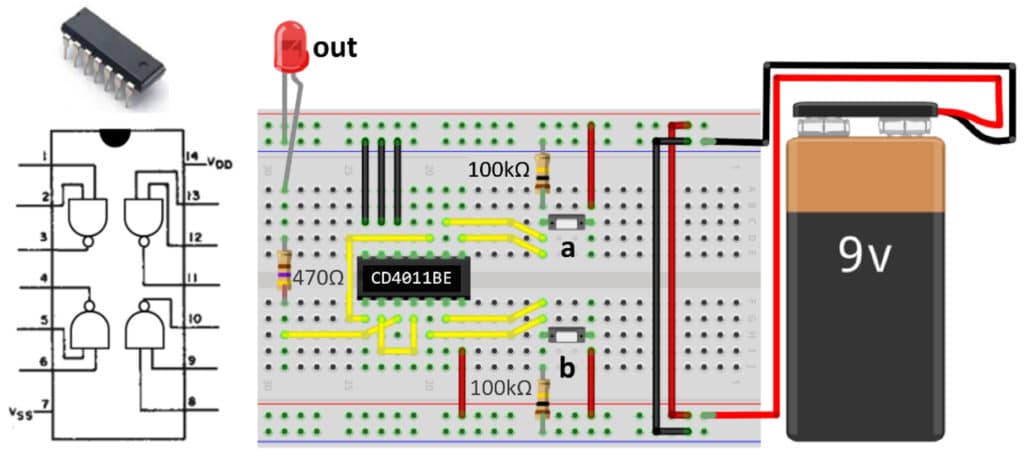
In der Schaltung in Abb.4 wird der CD4011BE-Baustein genutzt, um mit drei seiner NAND-Gatter ein OR-Gatter aufzubauen. Dazu wird der folgende Ausdruck verwendet:

a OR b = (a NAND a) NAND (b NAND b)

Die beiden Taster in der Schaltung stellen die Eingänge a und b dar. Im nicht-gedrückten Zustand werden ihre vom Pluspol der Stromquelle abgewandten Kontakte über einen hochohmigen Widerstand von 100kΩ auf Masse (Minuspol) gezogen. Die LED stellt den Ausgang der Schaltung dar. Sie wird durch einen Vorwiderstand von 470Ω vor einer Überlastung geschützt.

Auf die besondere Eigenschaft des NAND-Gatters als Universalgatter beziehen sich zwei aus pädagogischer und didaktischer Sicht besonders bemerkenswerte Projekte:

Das eine Projekt mit der Bezeichnung „From Nand toTetris“ (https://www.nand2tetris.org/) besteht aus zwei Teilen. Im ersten Teil werden unter Verwendung einer Hardwarebeschreibungssprache aus NAND-Gattern sukzessive alle notwendigen Schaltungen und Hardwarekomponenten für ein virtuelles Computersystem erstellt und zu einem solchen System kombiniert. Für dieses virtuelle System wird auch eine Maschinensprache definiert und ein Assembler entwickelt. Im zweiten Teil werden dazu ein Betriebssystem und ein Compiler samt virtueller Laufzeitumgebung für eine Java-ähnliche Programmiersprache erstellt. Damit werden dann Spiele wie Tetris und Pong programmiert, welche auf diesem selbst erstellten, nur auf NAND- Gattern beruhenden, virtuellen Computersystem gespielt werden können. Das virtuelle Computersystem wird mit speziell für  das Projekt programmierten Java-Anwendungen realisiert.  Es existieren dazu auf Coursera auch zwei frei zugängliche und didaktisch ausgezeichnet gestaltete MOOCs (https://www.coursera.org/learn/build-a-computer und https://www.coursera.org/learn/nand2tetris2).

Das zweite Projekt mit der Bezeichnung „Nandgame“ bezieht sich auf das Erstgenannte: „The Nand Game is inspired by the amazing course From NAND to Tetris – Building a Modern Computer From First Principles which is highly recommended.“ (https://nandgame.com/) Es kann direkt in einem Browser „gespielt werden“. Es müssen dabei eine ganze Reihe von, wiederum nur auf NAND-Gattern basierende, Schaltungen erstellt werden, welche in mehrere Levels zusammengefasst sind. Der Level „Logic Gates“ ist der Ausgangspunkt. Über die Levels „Arithmetics“, „Switching“, „Arithmetic Logic Unit“ und „Memory“ gelangt man schließlich zum Level „Processor“, in dem abschließend ein schematisierter Computer erstellt werden muss. Jede zu erstellende Schaltung wird durch eine genaue Spezifikation beschrieben. Abb.5 zeigt ein mit Nandgame unter Verwendung des folgenden Ausdrucks erstelltes XOR-Gatter:

a XOR b = (a NAND (a NAND b)) NAND ((b NAND (a NAND b))

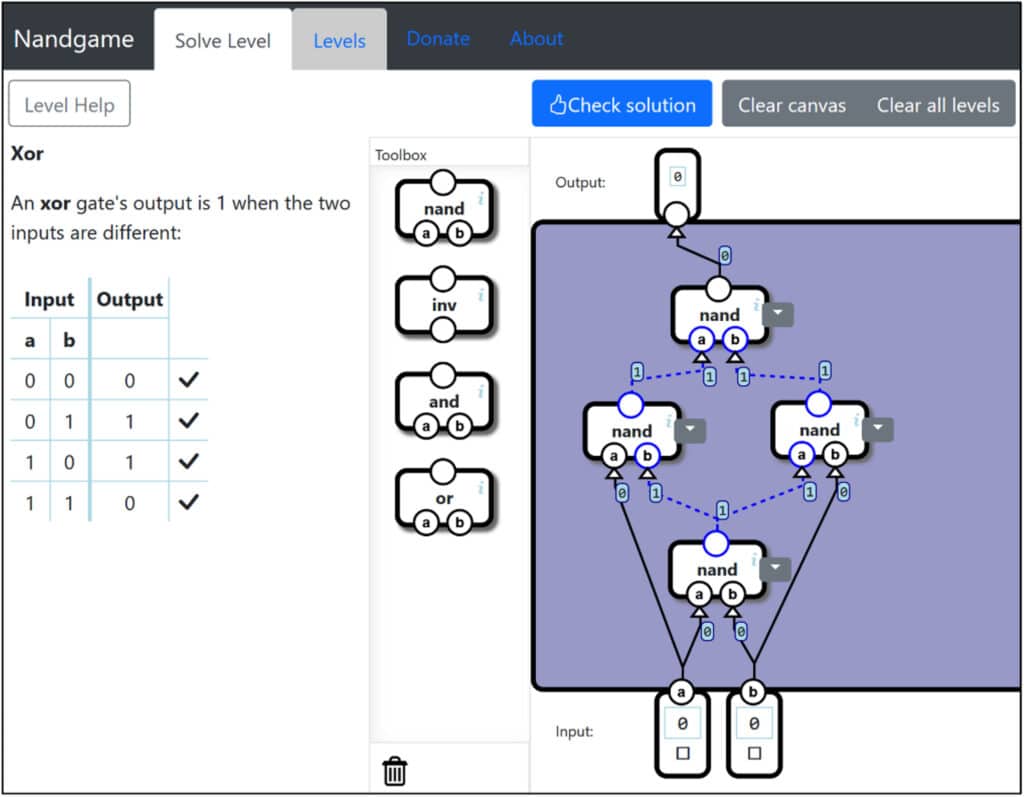
Die violette Fläche stellt das IC-Gehäuse dar. Die Anschlüsse außerhalb dieser Fläche (Input: a, b und Output) sind vorgegeben. Zum Aufbau einer Schaltung müssen aus dem Toolbox-Bereich die passenden Elemente in das IC-Gehäuse gezogen und miteinander verbunden werden. Über die Schaltfläche mit der Aufschrift „Check solution“ kann die richtige Funktionsfähigkeit der Schaltung überprüft werden.

Arithmetik-Schaltungen

Die Durchführung arithmetischer Operationen gehört zu den Kernaufgaben eines jeden Computersystems. Besonders bemerkenswert ist dabei, dass sich alle vier Grundrechnungsarten im Prinzip nur mit einer Addierer-Schaltung realisieren lassen: Eine Subtraktion kann als Addition mit einem negativen Summanden, eine Multiplikation als mehrfache Addition und eine Division als mehrfache Subtraktion ausgeführt werden.

Um Mehrbit-Werte zu addieren, werden Volladdierer-Schaltungen benötigt. Ein Volladdierer hat die Aufgabe, die Addition zweier Eingangsbits (a und b) sowie eines Carry-Eingangsbits (ci), welches als Übertrag von einer Stelle weiter rechts anfallen kann, auszuführen. Am Ausgang werden ein Summationsbit (sum) sowie eine Carry-Ausgangssignal (co) bereitgestellt. Ein Volladdierer kann mit zwei XOR-Gattern, zwei AND- Gattern und einem OR-Gatter aufgebaut werden.

Die Volladdierer-Schaltung in Abb.6 wurde mit Logicly (https://logic.ly/) erstellt. Dabei handelt es sich um eine sehr einfach und intuitiv zu bedienende Schaltungssimulationssoftware, welche als freie Online-Version zur Verfügung steht und auch als kostenpflichtige App angeboten wird.

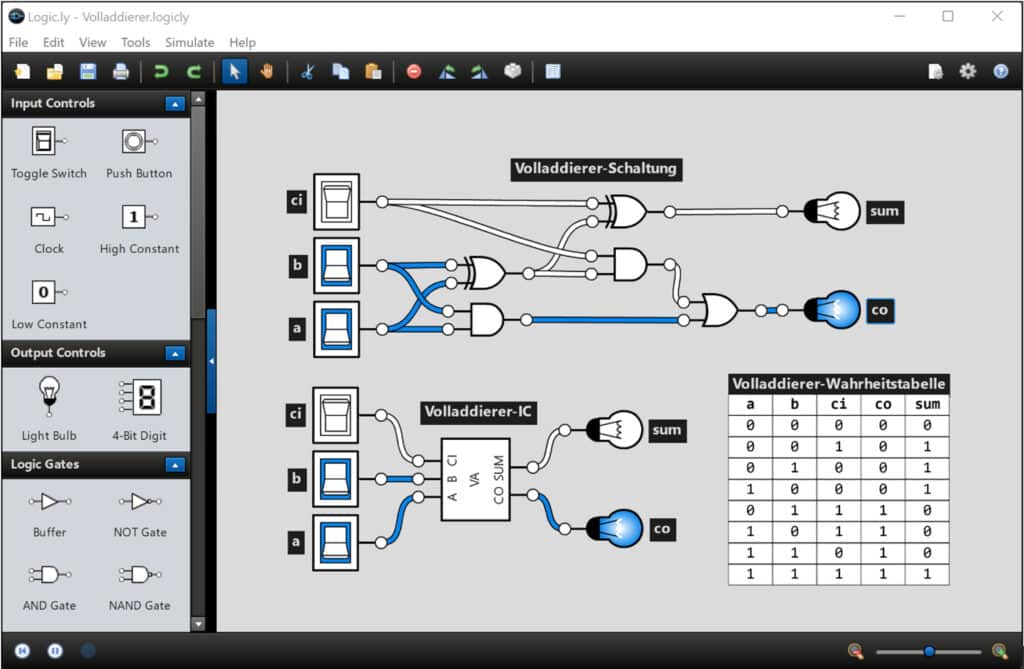
Bei Logicly können als Eingangssignalgeber Toggle-Switches verwendet werden, welche sich ein- und ausschalten lassen. Ausgangssignale können mit Light-Bulbs dargestellt werden. Im linken Fensterbereich finden sich im Abschnitt „Logic Gates“ die üblichen Logikgatter im ANSI-Format. Diese können in den Workspace gezogen, dort passend angeordnet und mit anderen Schaltungskomponenten sehr einfach verbunden werden. Wie in Abb.6 gezeigt, ist es mit Logicly auch möglich, eine erstellte Schaltung als integrierten Schaltkreis (IC) mit eigenem Gehäuse abzuspeichern. Die Anschlüsse können dabei selbst benannt und am IC-Gehäuse auch selbst positioniert werden. Mit einem Doppelklick auf einen solchen IC wird dessen interner Aufbau dargestellt. Sind darin weitere benutzerdefinierte ICs enthalten, so lässt sich auch deren Struktur mit weiteren Doppelklicks betrachten.

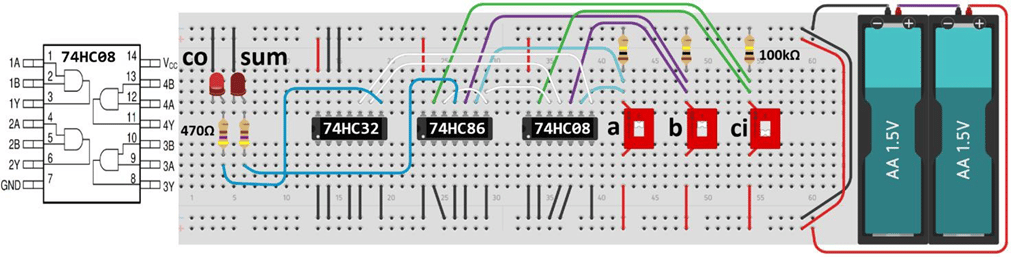
Abb.7 zeigt, wie diese Volladdierer-Schaltung mit Tinkercad-Circuits aufgebaut werden kann. Dabei kommen die drei ICs 74HC32 (mit vier OR-Gates), 74HC86 (mit vier XOR-Gates) und 74HC08 (mit vier AND-Gates) zum Einsatz, welche als eigene Bausteine vorhanden sind. Sie gehören zur 74HCxx- IC-Familie, deren Vertreter mit 2 bis 6 V Spannung betrieben werden können. HC steht dabei für „Highspeed CMOS“. In Abb.7 wird auch die Pinbelegung des 74HC08 gezeigt, die beiden anderen ICs sind ebenso aufgebaut. In der Schaltung sind die nicht verwendeten Gatter der drei ICs jeweils auf Masse gezogen. Im Simulationsmodus von Tinkercad-Circuits kann mit dieser Schaltung die Wahrheitstabelle des Volladdierers verifiziert werden.

Mit Hilfe von Volladdieren ist man in der Lage, ein vollständiges Addierwerk aufzubauen. Abb.8 zeigt einen 8-bit Addierer, erstellt mit Logicly.

Für jede Bitstelle wird dabei eine eigene Volladdierer-Komponente benötigt. Die jeweiligen Operanden-Bits von a und b werden jeweils an die a- und b-Eingänge der einzelnen Volladdierer geführt. Ein eventueller Carry-Eingang für den gesamten Addierer wird an den Carry-Eingang der niederwertigsten Stufe gelegt (ci), andernfalls wird dieser mit logisch 0 verbunden. Die Carry-Ausgänge der einzelnen Volladdierer werden in einer Kette mit den Carry-Eingängen der weiter links nachfolgenden Stufen verbunden. Der Carry-Ausgang (co) der letzten Volladdierer-Stufe kann als höchstwertiges Summationsbit interpretiert werden. Das Summationsergebnis ist damit zur Vermeidung von Überläufen um ein Bit breiter als die Operanden.

Abb.9 zeigt einen 8-bit Addierer aufgebaut auf einem Steckbrett. Dabei werden zwei 4-bit Volladdierer MC14008B-ICs eingesetzt.

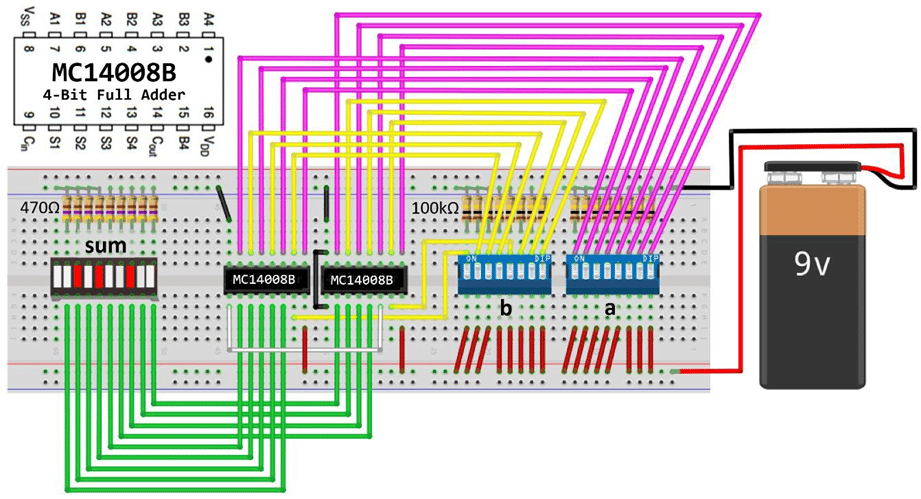
Die beiden Summanden a und b werden über DIP-Switches eingegeben, die errechnete Summe wird über einen LED-Bar-Baustein ausgegeben. Die Pin-Zuordnung des MC14008B ist in Abb.9 links oben dargestellt. Die Versorgungsspannung muss zwischen V_DD (+Pol) und V_SS (-Pol) angelegt werden. Die Summanden werden über die Eingänge A1 – A4 sowie B1 – B4 angeschlossen, die Summenbits werden an den Pins S1 – S4 ausgegeben. C_in ist der Übertrag-Bit-Eingang und C_out der Übertrag-Bit-Ausgang. Das C_in-Signal des rechten ICs ist auf Masse gezogen (logisch 0). Beim linken IC ist C_in mit C_out des rechten ICs verbunden. C_out des linken ICs ist als höchstwertiges Summationsbit mit dem LED-Bar-Baustein verbunden. Es wird die Addition 82 + 82 = 164 dargestellt.

Werden negative Zahlen im Binärsystem über das Zweierkomplement gebildet, kann die Differenz a – b direkt auf die Addition mit dem negativen Summanden (-b) zurückgeführt werden (a + (-b)). Somit lässt sich eine Addierer auch als Subtrahierer verwenden. Man erhält die Zweierkomplementdarstellung einer negativen Zahl, indem man alle Bitstellen ihrer binären Absolutbetragsdarstellung invertiert und abschließend eine 1 addiert.

Abb.10 zeigt einen mit Logicly erstellten 8-bit Addierer und Subtrahierer.

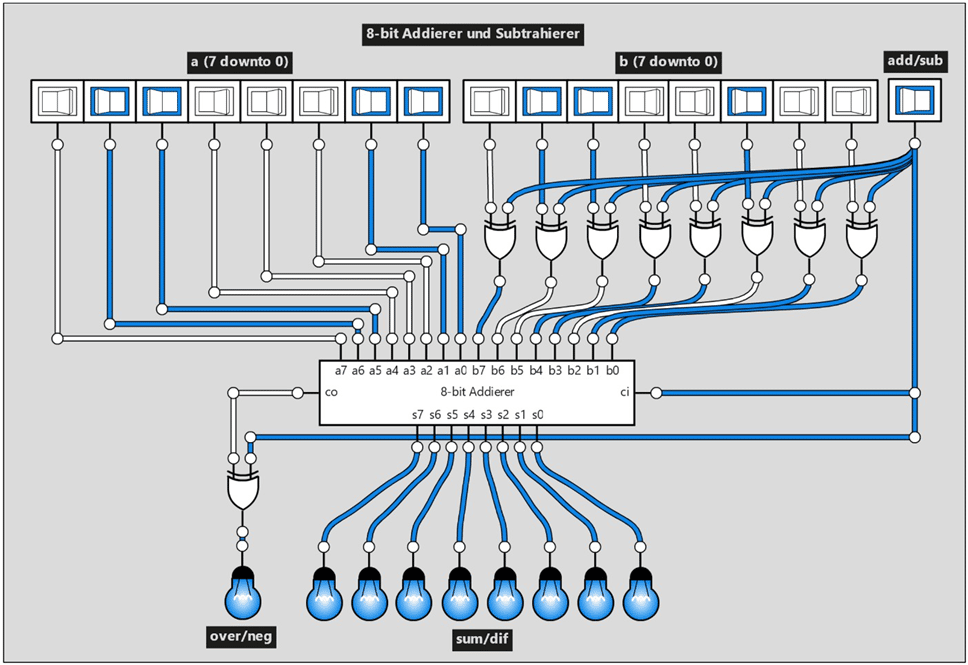
Die Werte für a und b werden jeweils über 8 Toggle-Switches angegeben. Das add/sub-Signal bestimmt die Art der Rechenoperation (0 Addition, 1 Subtraktion). Im Falle einer Subtraktion (add/sub = 1) wird von b das Zweierkomplement gebildet. Dabei erfolgt die Inversion von b mit acht XOR-Gatter und die Addition von 1 wird durch die Einspeisung des add/sub-Signals in den ci-Eingang des Addierers bewerkstelligt. Das Ergebnis (Summe oder Differenz) wird über acht Light-Bulbs ausgegeben (sum/dif). Ein Ausgabewert von 1 bei over/neg bedeutet im Falle einer Addition einen Überlauf (Summe > 255) und bei einer Subtraktion einen negativen Ergebniswert (Differenz < 0).

Datenflusskontrolle

Bei digitalen Schaltungen ist es oft erforderlich, den Datenfluss gezielt zu steuern. Dies kann mit Multiplexern und Demultiplexern erfolgen.

Multiplexer kommen immer dann zum Einsatz, wenn eine Signalleitung mit einem Wert beschaltet werden soll, der aus mehreren Quellen stammen kann. Ein Multiplexer führt diese Datenpfade gezielt zusammen. Dabei kann über Steuerleitungen bestimmt werden, welche der verschiedenen Eingangsleitungen, auf die eine Ausgangsleitung durchgeschaltet wird. Demultiplexer bewirken im Gegensatz dazu eine kontrollierte Aufspaltung von Datenpfaden. Über Steuerleitungen kann festgelegt werden, mit welcher der verschiedenen Ausgangsleitungen, die eine Eingangsleitung verbunden wird.

Abb.11 zeigt mit Logicly erstellte Multiplexer- und Demultiplexerschaltungen.

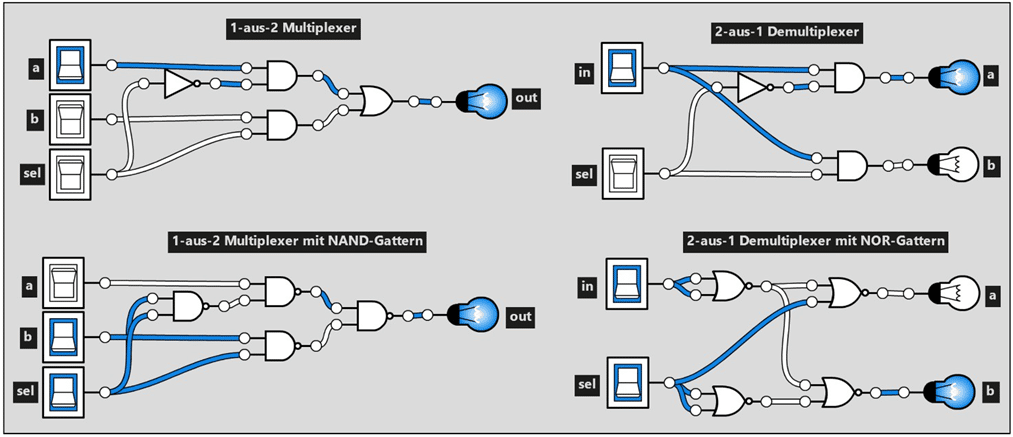
Die beiden Schaltungen auf der linken Seite in Abb.11 sind 1-aus-2 Multiplexer (2:1 MUX). Bei diesen kann mit dem sel-Signal bestimmt werden, ob der a-Eingang oder der b-Eingang auf den out-Ausgang durchgeschaltet wird. Ist das sel-Signal gleich 0 wird a mit out verbunden (links oben), ist sel gleich 1, wird b auf out gelegt (links unten). Beide Schaltungsvarianten sind funktionsgleich, bei der unteren Variante werden ausschließlich NAND-Gatter verwendet. Abb.12 zeigt diese Schaltung auf einem Steckbrett (links). Dabei wird ein CD4011BE-IC mit vier NAND-Gattern verwendet.

Auf der rechten Seite in Abb.11 befinden sich zwei 2-aus-1 Demultiplexerschaltungen (1:2 DEMUX). Das sel- Signal bestimmt dabei, ob das in-Signal auf den a-Ausgang oder den b-Ausgang durchgeschaltet wird. Ist das sel-Signal gleich 0, so wird das in-Signal auf den a-Ausgang gelegt (rechts oben), ist sel gleich 1, wird das in- Signal mit dem b-Ausgang verbunden (rechts unten). Wiederum sind beide Schaltungen funktionsgleich. Bei der unteren Variante werden nur NOR-Gatter eingesetzt. Wie sich diese Schaltung auf einem Steckbrett realisieren lässt, wir in Abb.12 rechts gezeigt. Dabei wird ein CD4001BE-ICs mit vier NOR-Gattern verwendet.

Neben den hier vorgestellten einfachen Varianten werden in der Praxis auch häufig deutlich größere und kompliziertere Multiplexer- und Demultiplexer-Bausteine verwendet. Einerseits können die Ein- und Ausgangsignalleitungen (in, a, b, out) breiter sein (8-bit, 16-bit, 32-bit, …), andererseits sind mit mehreren Steuerleitungen (sel1, sel2, …) auch mehrere Ein- und Ausgangssingale möglich (n:1 MUX bzw. 1:n DEMUX).

ALU

In den vorangegangenen Abschnitten wurden wichtige Grundkomponenten digitaler Schaltungen vorgestellt, die sich in modernen Mikroprozessoren auf die eine oder andere Weise wiederfinden. Einige dieser Komponenten sind als arithmetisch-logische Einheit (ALU – Arithmetic Logic Unit) zusammengefasst. Diese stellt unterschiedliche arithmetische und logische Funktionen bereit, welche über Steuerleitungen ausgewählt werden können.

Im Folgenden wird die 16-bit ALU des „From Nand To Tetris“-Projekts (https://www.nand2tetris.org/) vorgestellt. Diese ALU ist relativ einfach aufgebaut. Sie bewältigt aber alle notwendigen Berechnungen bei der Ausführung der im Rahmen dieses Projektes entwickelten Spiele Tetris und Pong einwandfrei. Abb.13 gibt einen Überblick über ihre Anschlüsse und Funktionen.

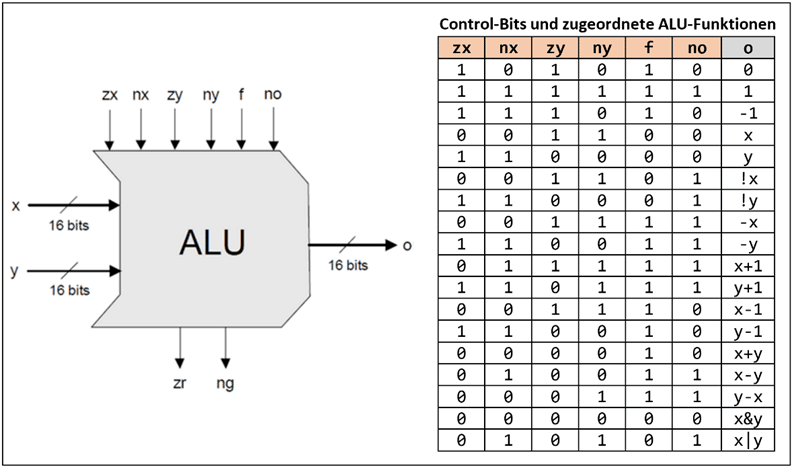
Die ALU besitzt zwei 16-bit Eingänge (x und y), einen 16-bit Ausgang (o), sechs 1-bit-Steuereingänge (zx, nx, zy, ny, f und no) und zwei 1-bit Ausgänge zur Ausgabestatusanzeige (zr: 1 bei o=0, ng: 1 bei o<0). Die sechs 1-bit Steuereingänge (Control-Bits) bestimmen die von der ALU ausgeführte Operation. Über sie kann eine von 18 Funktionen ausgewählt werden. Diese Funktionen sind in Abb.13 mit den dafür vorgesehenen Control-Bit-Werten aufgelistet. In den Computation-Instructions des 16-bit Maschinencodes des „From Nand To Tetris“-Systems sind für diese Steuereingänge sechs Bits als ALU-Opcode   vorgesehen. Die Maschinenbefehle werden innerhalb der Control Unit der CPU ausgewertet und je nach ermitteltem Opcode wird die entsprechende Funktion der ALU aktiviert.

Abb.14 zeigt den internen Aufbau der „From Nand To Tetris“-ALU.

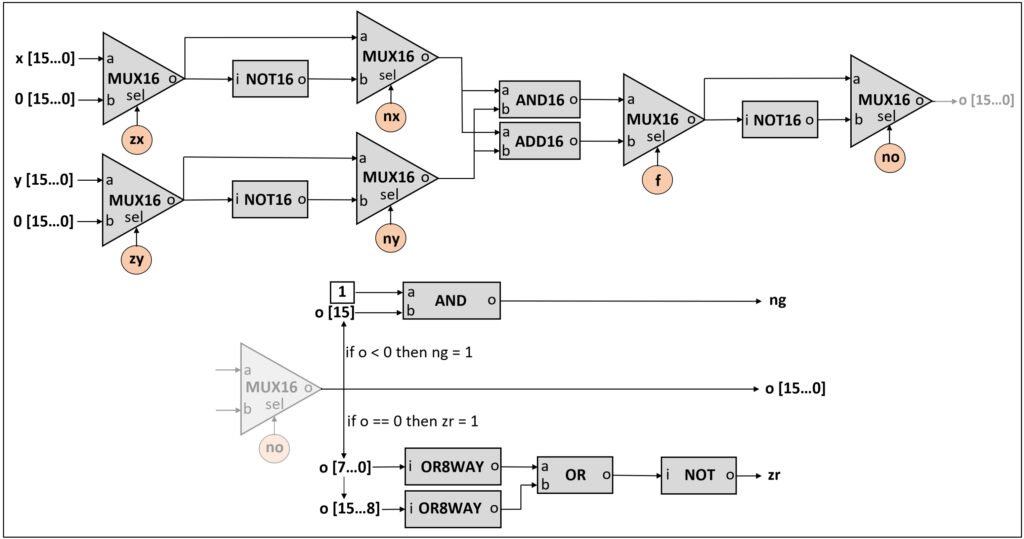
Im oberen Teil von Abb.14 ist der Datenpfad von den Eingangssignalen x und y zum Ausgangssignal o dargestellt, der untere Teil zeigt detailliert die schaltungstechnische Realisierung der Statusausgaben ng und zr. In der „From Nand To Tetris“-ALU sind die folgenden Komponenten enthalten:

• 6x MUX16 (16-bit 1-aus-2 Multiplexer)
  Diese Multiplexer verfügen jeweils über einen 1-bit Selektionssignaleingang (sel), mit dem eines der beiden 16-bit Eingangssignale (a oder b) ausgewählt und an den 16-bit Ausgang (o) durchgeschalten werden kann. Bei sel=0 wird a nach o durchgeschalten, bei sel=1 wird b ausgegeben. Jedes der sechs ALU-Steuersignale (zx, nx, zy, ny, f und no) dient als Selektionssignal bei einem dieser sechs Multiplexer.

• 3x NOT16 (16-bit NOT-Gatter)
  Diese nehmen jeweils am Eingang i einen 16-bit Wert entgegen und geben diesen als invertierten 16-bit Wert am Ausgang o aus.

• 1x AND16 (16-bit AND-Gatter) und 1x ADD16 (16-bit Addierer)
  AND16 ist ein Baustein, welcher die beiden 16-bit Eingänge a und b bitweise „UND-verknüpft“ und das Ergebnis beim Ausgang o als 16-bit Wert ausgibt. ADD16 ist ein 16-bit Addierer mit den 16-bit Eingängen a und b für die beiden Summanden und dem 16-bit Ausgang o für die errechnete Summe.

• 2x OR8WAY, 1x OR, 1x NOT und 1x AND
  Diese Bausteine dienen zur Ermittlung der Statusausgaben (zr und ng) der ALU. zr ist 1, wenn der von der ALU bei o ausgegebene Wert 0 ist, ansonsten 0. ng ist 1, wenn der von der ALU bei o ausgegebene Wert negativ ist, ansonsten 0.

Abb.15 zeigt die „From Nand To Tetris“-ALU als IC, erstellt mit Logicly. Bei den Steuersignalen ist nur das f-Control-Bit aktiviert. Es erfolgt daher eine Addition (vgl. Abb.13).

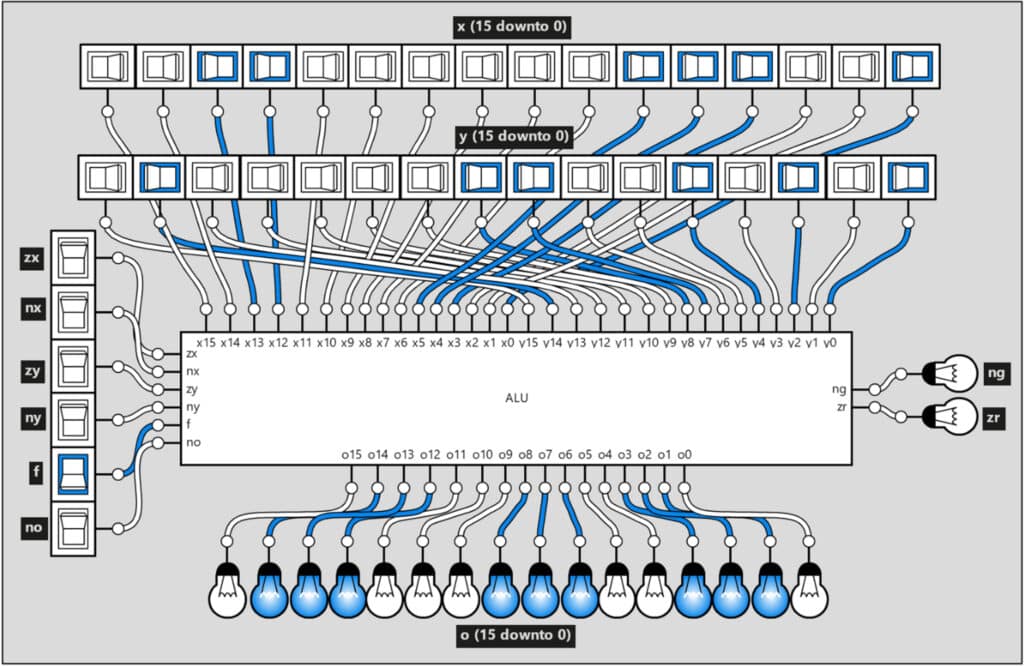
Die Erstellung des 16-bit ALU-ICs in Abb.15 ist relativ aufwendig. Die Logicly-App unterstützt aber eine arbeitsteilige Vorgangsweise. Schaltungskomponenten können erstellt und als IC-Bibliotheksdateien exportiert und importiert werden. Schaltungsteile können auch mittels Copy & Paste zwischen App-Instanzen ausgetauscht werden.

ALU in FPGA-Implementierung

Eine Schaltung wie die ALU des „From-Nand-To-Tetris“-Projekts lässt sich auf Steckbrettern kaum mehr sinnvoll aufbauen. Eine Möglichkeit der physischen Umsetzung eröffnen in diesem Zusammenhang FPGA-Boards. FPGA steht für „Field Programmable Gate Array“, was so viel wie „im Feld (vor Ort durch den Benutzer) programmierbare Logikgatter-Anordnung“ bedeutet.

Ein FPGA-Chip enthält – sehr vereinfacht dargestellt – Logikblöcke, die nicht wie in herkömmlichen Mikrochips fest verdrahtet sind, sondern durch das Implementieren einer Konfigurationsdatei miteinander verbunden werden. In diesen Chips lassen sich also eigene digitale Schaltungen aufbauen und sie können immer wieder neu konfiguriert werden, auch mit unterschiedlichen Schaltungen.

Die Erstellung von FPGA-Konfigurationsdateien erfolgt mit speziellen Konfigurationssprachen. VHDL (Very High Speed Integrated Circuit Hardware Description Language) ist eine solche Sprache. VHDL-Dateien können in einem Texteditor geschrieben und müssen dann von einer Synthese-Software in eine Bitstream-Datei übersetzt werden. Diese kann dann in den FPGA-Chip geladen und damit die gewünschte Schaltung realisiert werden.

Im Folgenden wird die Implementierung der „From-Nand-To-Tetris“-ALU auf einem Terasic DE0-CV FPGA- Board (https://www.terasic.com.tw/) kursorisch beschrieben. Als Synthese-Software wird die kostenlos erhältliche Intel Quartus Prime Lite Edition verwendet (https://fpgasoftware.intel.com/?edition=lite). Darin ist auch Intel ModelSim, Starter Edition enthalten, eine Simulations- und Testumgebung für mit Hardwarebeschreibungssprachen wie VHDL erstellte Schaltungen.

Das Terasic DE0-CV Board ist mit einem Intel (vormals Altera) FPGA Chip Cyclone V Typ 5CEBA4F23C7 ausgestattet. Dieser verfügt u.a. über 49K programmierbare Logikelemente. Auf dem Board befinden sich viele Peripheriekomponenten, welche für eigene Schaltungen genutzt werden können.

Abb.16 zeigt den verwendeten Aufbau zur Implementierung der „From Nand To Tetris“-ALU.

Von den Board-Komponenten werden die sechs 7-Segment-Anzeigen zur Ergebnisausgabe im dezimalen Format (o), die darunter befindlichen Switches zur Eingabe der Control-Bits (zx, nx, zy, ny, f, no), die darüber befindlichen LEDs zur Anzeige der gesetzten Control-Bits und der beiden Ausgabestatusbits (ng, zr) sowie eine der beiden GPIO-Schnittstellen (GPIO_1) zur Eingabe der beiden Operanden (x, y) genutzt. Die Eingabe der Operanden erfolgt dabei über jeweils zwei 8-polige DIP-Schaltermodule auf einem Steckbrett. Die Verbindung zur GPIO-Schnittstelle des Boards kann über ein Flachbandkabel, ein 40-Pin GPIO-Breakoutboard und flexible Steckbrücken hergestellt werden. Die GPIO-Schnittstelle des Boards liefert 5V auf Pin 11, 3.3V auf Pin 29 sowie GND auf Pin 12 und Pin 30. Masseseitig befinden sich bei den DIP-Schaltern 100kΩ-Widerstände.

Mit VHDL können Schaltungen auf verschiedenen Abstraktionsebenen entworfen werden, von einer funktionalen Verhaltensbeschreibung auf höchster Ebene bis zu einer rein strukturellen Beschreibung auf Gatterebene. Für die Implementierung der „From Nand To Tetris“-ALU ist ein Strukturmodell adäquat. Der in Abb.14 wiedergegebenen Aufbau der ALU soll damit möglichst genau abgebildet werden.

In einem VHDL-Strukturmodell wird eine Schaltung als Entität definiert, deren Struktur durch die Instanziierung der in der Schaltung enthaltenen Komponenten und deren Verbindungen beschrieben wird. Jede verwendete Komponente muss mit ihren Schnittstellen vorweg angeführt werden und mit einem eigenen VHDL-Modell vorliegen. Zur Verbindung der einzelnen   Komponenten werden Signale definiert.

Abb.17 und Abb.18 zeigen die VHDL-Beschreibung der „From Nand To Tetris“-ALU.

Der VHDL-Code gliedert sich in mehrere Abschnitte:

• Zeile 1 in Abb.17 ist eine Kommentarzeile, Kommentare beginnen in VHDL mit der Zeichenkette „–„. Wie alle Code-Dateien, sollen auch VHDL-Dateien ausführlich mit Kommentaren versehen werden. Um den Inhalt zu verkürzen, wurden diese hier entfernt. Zeile 2 ist eine Leerzeile. Whitespaces sowie Groß- und Kleinschreibung haben bei VHDL keine syntaktische Bedeutung.

• Mit Zeile 3 in Abb.17 wird die Bibliothek „ieee“ eingebunden und in Zeile 4 darauf Bezug genommen. In der IEEE-Bibliothek ist u.a. der Datentyp „std_logic“ definiert, der zur Beschreibung von Anschlüssen (Ports) und Signalen in der Regel verwendet wird. Er stellt eine Erweiterung des Datentyps „bit“ dar und kann neben den beiden Werten „0“ und „1“ noch weitere Werte wie z.B. „U“ für „Uninitialized“ annehmen.

• Von Zeile 6 bis 20 in Abb.17 wird die Schaltung als Entität „alu“ definiert. Darin erfolgt mit dem port- Statement die Beschreibung aller ihrer Ein- und Ausgänge. Diese „Kommunikationskanäle“ oder Ports werden jeweils mit Bezeichner, Signalflussrichtung und Datentyp festgelegt. Als Datentyp wird in der Regel „std_logic“ verwendet. Mit „std_logic_vector“ werden Ports definiert, die mehr als 1 Bit breit sind. Der Ausdruck „15 downto 0“ gibt an, dass 16 Bits verwendet werden und das Bit mit dem Index 15 das Höchstwertige ist. Diese Zeilen sind im Grunde eine textuelle Beschreibung aller Ein- und Ausgänge der ALU, genauso wie in Abb.13 grafisch dargestellt.

• Mit dem architecture-Statement in Zeile 22 in Abb.17 wird die strukturelle Beschreibung der ALU-Schaltung eingeleitet. Vorweg werden darin zunächst in den Zeilen 23 bis 76 alle verwendeten Schaltungskomponenten mit ihren Schnittstellen als Prototypen angeführt. Im Detail sind dies ein 16-bit 1-aus-2 Multiplexer (mux2way16), ein 16-bit NOT-Gatter (not16), ein 16-bit AND-Gatter (and16), ein 16-bit Addierer (add16), ein AND-Gatter (and_gate), ein 8-Bit Mehrweg-OR-Gatter (or8way), ein OR-Gatter (or_gate) und ein NOT-Gatter (not_gate). Wie aus Abb.14 hervorgeht, sind alle diese Bausteintypen für den Aufbau der ALU erforderlich. Ihre Schnittstellen werden wie bei der Entity-Definition mit dem port-Statement beschrieben. Für alle diese Bausteintypen muss jeweils auch ein eigenes VHDL-Modell in einer eigenen VHDL-Datei vorhanden sein, damit die Simulations- und Syntheseprogramme (ModelSim und Quartus) deren interne Strukturen auflösen können.

• In den Zeilen 78 bis 91 in Abb.18 werden mit dem signal-Statement vorweg 14 Signalleitungen definiert. Diese werden später zum Verbinden der einzelnen Schaltungskomponenten benötigt. Dabei werden jeweils ein Bezeichner und ein Datentyp angegeben.

• In den Zeilen 93 bis 111 in Abb.18 wird die Struktur der Schaltung beschrieben. Dabei werden Instanzen der vorher angegebenen Bausteinprototypen erstellt und diese mittels der vorher definierten Signalleitungen verbunden. Diese Zeilen sind im Grunde eine textuelle Beschreibung des in Abb.14 grafisch dargestellten internen Aufbaus der ALU. In Zeile 94 wird mit „i_mux1 : mux2way16“ ein 16-bit 1-aus-2 Multiplexer instanziiert. Dieser befindet sich in Abb.14 links oben. Mit dem „port map“- Statement werden dessen Ein- und Ausgänge konfiguriert. Eingang a wird an den Operanden x der ALU angeschlossen (a => x), Eingang b mit der Konstanten 0 (b => „0000000000000000“), der sel-Eingang mit dem Control-Bit zx der ALU (sel => zx) und o mit dem Signal mux1_s (o => mux1_s) verbunden. Das Signal mux1_s wird in den Instanzen i_not1 und i_mux_2 jeweils als Eingang verwendet. In dieser Form wird die Struktur und der Datenpfad der ALU fortlaufend beschrieben, bis schließlich in den Zeilen 105, 106 und 110 die ALU-Ausgänge o, ng und zr beschalten werden.

In einem nächsten Schritt sollte die entworfene Schaltung mittels Simulation getestet werden. Dazu wird die Software ModelSim und eine sogenannte Testbench verwendet. Eine Testbench ist eine VHDL-Datei, welche das Modell der entworfenen Schaltung einbindet und der Reihe nach mit unterschiedlichen Eingangssignalen konfrontiert. Als Ergebnis erhält man einen  Plot von Ein- und Ausgangssignalen mit dem die richtige Funktionsfähigkeit der Schaltung überprüft werden kann.

Abb.19 zeigt einen Ausschnitt eines solchen Plots. In diesem werden mit den Eingabe-Werten x_s=17 und y_s=3 für die beiden Operanden und den Control-Bit-Eingaben für die ALU-Funktionen x + y (zx_s=0, nx_s=0, zy=0, ny_s=0, f_s=1, no=0), x – y, y – x, x & y sowie x | y die von der Schaltung ausgegebenen Ergebnisse (o_s) nacheinander von links nach rechts angezeigt. In der Spalte „Msgs“ werden alle Signalwerte in numerischer Form für die Position ausgegeben, an der sich der gelbe Balken gerade befindet (x + y). Der Balken kann mit der Maus verschoben werden.

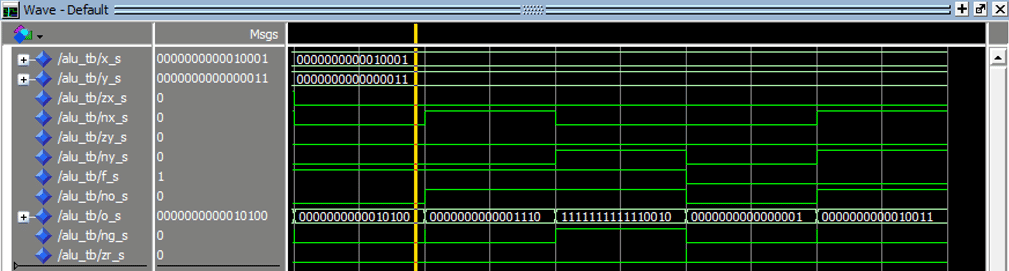
Nach der erfolgreichen Simulation und Testung der Schaltung mit ModelSim, folgt deren Implementierung auf dem FPGA-Board. Dazu wird die Entwicklungsumgebung Quartus Prime verwendet. Abb.20 zeigt das Anwendungsfenster.

Es muss dafür ein neues Quartus Prime-Projekt angelegt und diesem müssen neben der Datei mit dem VHDL-Modell der ALU auch die VHDL-Dateien aller verwendeten Schaltungskomponenten hinzugefügt werden. Darüber hinaus ist noch eine weitere VHDL-Datei erforderlich.

In dieser Datei werden die verwendeten Board-Komponenten (GPIO-Schnittstelle, Switches, LEDs und 7-Segment-Displays) mit ihren Ports als Top-Level-Entity definiert (alu_de0cv), die ALU-Schaltung als Komponente (alu) eingebunden, instanziiert (i_alu) und mit den Ports der Board-Komponenten verbunden. Neben der ALU sind in dieser Datei noch zwei weitere Schaltungskomponenten enthalten. Die Komponente bin16s2bcds dient zur Umwandlung der binären ALU-Ausgabe in das dezimale Format. Die Komponente bcds2sseg wird zur Darstellung der dezimalen Ziffern auf den 7-Segment-Displays benötigt. In Abb.20 sind links oben im Bereich „Project Navigator“ alle Komponenten der Schaltung alu_de0cv mit ihren Instanzen angeführt. Das Editorfenster rechts daneben zeigt den oberen Teil der Datei alu_de0cv.vhd mit der (teilweise verdeckten) Entity-Definition.

Bevor die zur Konfiguration des FPGA-Chips erforderliche Bitstream-Datei erstellt werden kann, muss noch die Zuordnung der Ports der Board-Komponenten zu den Pins des FPGA-Chips vorgenommen werden. Dies kann mit Hilfe einer Assignment-Datei oder mit dem Quartus Pin Planner erfolgen.

Danach kann über die dreieckige Schaltfläche in der Buttonleiste des Anwendungsfensters die Kompilation des Designs durchgeführt werden. Der Fortschritt dieses Vorgangs lässt sich im „Bereich Tasks“ der Quartus- Umgebung mitverfolgen. In Abb.20 ist dieser links, unterhalb von „Projects Navigator“ zu sehen. Es werden dabei mehre Phasen durchlaufen. Falls Fehler auftreten, müssen diese beseitigt werden. Die erzeugte Bitstream-Datei wird im Projekt-Unterverzeichnis „output files“ gespeichert und hat die Bezeichnung der Top-Level-Entität mit der Dateierweiterung „sof“ (SRAM object file).

Als letzter Schritt erfolgt der Download des Bitstreams auf das Board. Dazu muss es per USB-Kabel mit dem Entwicklungscomputer verbunden sein. Zum Download wird der Programmer über die gleichnamige Schaltfläche gestartet. In Abb.20 ist rechts unten das Programmer-Dialogfenster zu sehen. Nachdem die Verbindung mit der auf dem Board vorhandenen USB-Blaster-Schnittstelle aufgebaut wurde, kann die Übertragung der Bitstream-Datei vorgenommen werden.

Damit ist das Terasic DE0-CV FPGA-Board als „From Nand To Tetris“-ALU konfiguriert. Über die DIP-Schalter auf dem Steckbrett können die beiden Operanden x und y eingegeben und über die Switches auf dem Board können die sechs Control-Bits zx, nx, zy, ny, f und no gesetzt werden, um eine der 18 Funktionen der ALU auszuwählen. Das von der ALU ermittelte Ergebnis wird auf den 7-Segment-Displays in dezimaler Form ausgegeben (vgl. Abb.16).

Der gesamte Implementierungsprozess ist ohne Zweifel arbeitsintensiv und zeitaufwendig. Der Unterricht muss daher je nach pädagogischer Zielsetzung entsprechend geplant und vorbereitet werden. Mit vorinstallierten und entsprechend vorkonfigurierten Systemen lässt sich der Arbeitsaufwand für die Lernenden deutlich verringern. Wenn es in erster Linie um einen „Einstieg in das Chipdesign“ geht, kann beispielsweise nur mehr das Vervollständigen der VHDL-Beschreibung der ALU sowie das Kompilieren und Übertragen auf das FPGA-Board als Aufgabenstellung verbleiben. Das mögliche Erfolgserlebnis, „seinen eigenen Mikrochip erstellt zu haben“, sollte dabei für eine entsprechende Motivation sorgen.

Digitale Speicherelemente

Alle bisher erörterten Schaltungen gehören in den Bereich der kombinatorischen Logik. Bei diesen Schaltungen sind die Signalwerte der Ausgangsleitungen unmittelbar und ausschließlich von den Signalwerten der Eingangssignale abhängig.  Sie verfügen über „kein Gedächtnis“. In der Digitaltechnik werden aber auch Schaltungen benötigt, welche Informationen speichern können. Diese Schaltungen werden als Schaltwerke bezeichnet und zählen zur sequenziellen Logik. Bei diesen werden die ausgegebenen Signale nicht nur durch die aktuell anliegenden Eingabewerte bestimmt, sondern auch durch den Zustand, in dem sich die Schaltung gerade befindet.

Wie lassen sich aus Logikgattern Informationsspeicher erstellen? Die Antwort auf diese Frage lautet: durch Rückkopplung. Dabei wird ein Ausgangssignal wieder zurück in einen Eingang der Schaltung geführt. Dieser Effekt lässt sich mit Logicly und der Schaltung in Abb.21 links oben sehr anschaulich demonstrieren. Nachdem der Button (s) einmal betätigt wurde, gibt das ODER-Gatter durch den Rückkopplungseffekt den Wert 1 aus, auch dann, wenn der Button nicht mehr gedrückt wird. Damit wird die Information „Button wurde gedrückt“ gespeichert. Was bei dieser Schaltung fehlt, ist eine Rücksetzungsmöglichkeit des Ausgangswerts (q) von 1 auf 0.

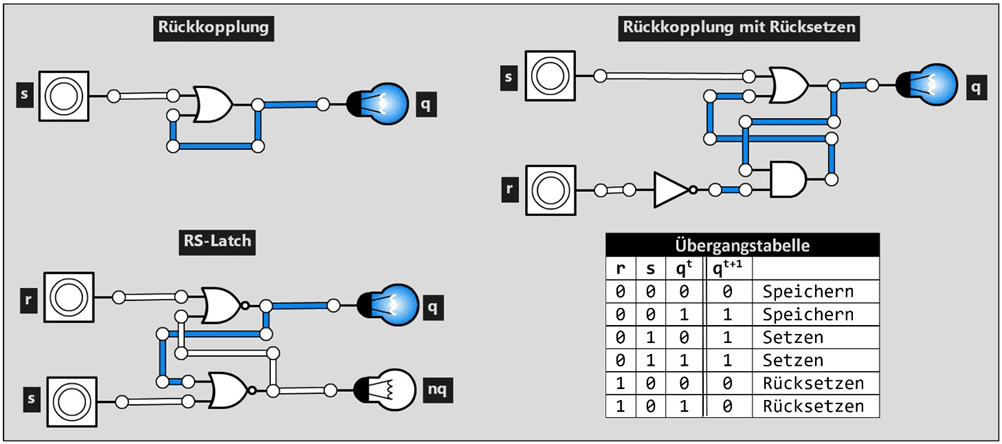
Dies kann, wie bei der Schaltung in Abb.21 rechts oben, durch das Hinzufügen eines NOT- und eines AND- Gatters erreicht werden. Beim Drücken des unteren Buttons (r) wird dessen Signalwert 1 durch das NOT-Gatter in den Wert 0 invertiert und damit liefert das nachgeschaltete UND-Gatter nicht mehr den Wert 1 sondern den Wert 0 an das ODER-Gatter. Nachdem der obere Button (s) nicht gleichzeitig gedrückt werden kann, haben nun beide Eingänge des ODER-Gatters den Wert 0 und damit nimmt auch dessen Ausgangssignal diesen Wert an, wird also zurückgesetzt. Beim Drücken des oberen Buttons wird wiederum die positive Rückkopplung aktiv. Eine solche Schaltung wird RS-Latch genannt. R steht dabei für Reset und S für Set.

Ein RS-Latch ist ein binärer Zustandsspeicher, d.h. es kann sich in einem von zwei Zuständen befinden, diese lassen sich auch mit 0 und 1 bezeichnen. In der Praxis wird ein RS-Latch häufig mit zwei rekursiv zusammengeschalteten NOR-Gattern implementiert. Die Schaltung in Abb.21 links unten zeigt diese Realisierungsform. Der aktuell eingenommene Zustand wird dabei am Ausgang q angezeigt. Der zweite Ausgang nq ist stets mit der Negation von q beschaltet und damit im Grunde überflüssig. Da dieser Wert aber ohnehin intern anfällt, wird er in den meisten Fällen auch nach außen geführt. In der Übergangstabelle des RS-Latches taucht die binäre Zustandsvariable q zweimal auf – einmal als aktueller Zustand q^t und einmal als Folgezustand q^t+1, in den das Latch übergeht, wenn es sich im Zustand q^t befindet und die Eingangssignale r und s anliegen. Die Kombination rs = 11 ist an den Eingängen eines NOR-implementierten RS-Latches zu vermeiden. Aufgrund der gatter- und leistungsbedingten Laufzeitverzögerung kann es dadurch in einen Schwingungszustand geraten.

Wie in Abb.22 rechts dargestellt, lässt sich ein solches RS-Latch unter Verwendung eines CD4001BE-ICs auf einem Steckbrett sehr einfach aufbauen. Dabei werden zwei seiner vier NOR-Gatter genutzt. Die Eingänge der nicht verwendeten Gatter werden auf Masse gezogen. Die beiden gelben Steckbrücken sind die rückgekoppelten Signalleitungen. Ein kurzes Drücken auf den rechten Taster (s) bringt die rechte LED (q) dauerhaft zum Aufleuchten.  Mit dem linken Taster (r) wird die linke LED  (nq)  anhaltend  aktiviert.

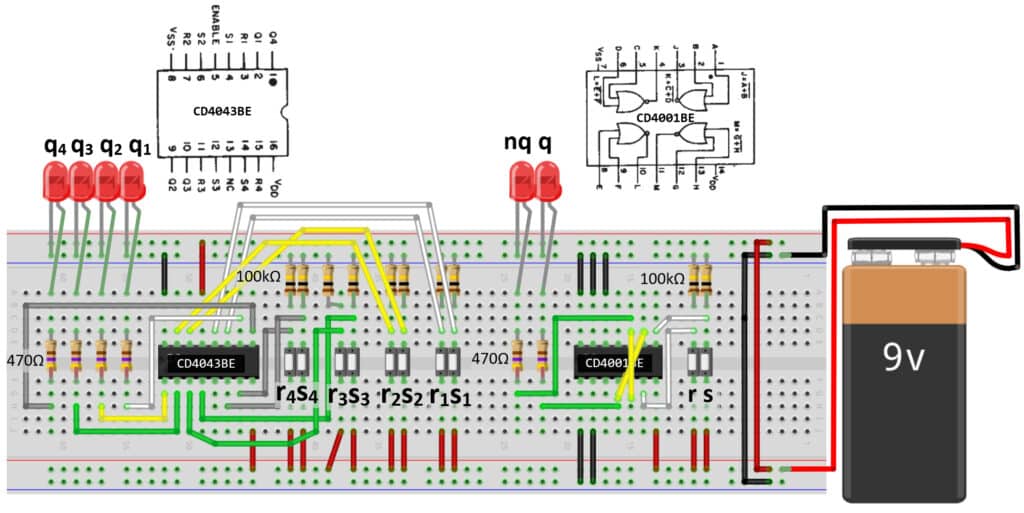
Die Schaltung in Abb.22 links verwendet den CD4043BE-IC. Dieser enthält vier RS-Latches auf NOR-Basis. Der Baustein verfügt nur über q- und keine nq-Ausgänge. Damit die q-Signalwerte ausgegeben werden, muss auch auf den Enable-Anschluss (Pin 5) die Versorgungsspannung (V_DD) gelegt werden. Mit den s- und r- Tastern können dann die zugehörigen LEDs anhaltend ein- und ausgeschaltet werden.

Bei den in Abb.21 und Abb.22 vorgestellten RS-Latches kann eine Zustandsänderung zu jeder beliebigen Zeit erfolgen. Diese Schaltungen werden aus diesem Grunde als asynchrone Speicherelemente bezeichnet. Im Gegensatz dazu sind bei   synchronen Schaltungen Zustandsänderungen nur innerhalb bestimmter Zeitintervalle möglich. Ein synchrones Schaltverhalten ist vor allem in Computersystemen wichtig. In diesen Systemen müssen die meisten Vorgänge zeitlich getaktet erfolgen. Nur so kann der beim Ausführen von Programmen ablaufende Von-Neumann-Zyklus funktionieren. Zur zeitlichen Synchronisation wird üblicherweise ein Taktsignal verwendet. Es entspricht einer periodischen Rechteckschwingung und wechselt zwischen den Signalwerten 0 und 1. Es wird dabei zwischen der positiven Taktphase (Signalwert 1) und der negativen Taktphase (Signalwert 0) sowie der positiven (steigenden) Taktflanke und der negativen (fallenden) Taktflanke unterschieden.

Abb.23 zeigt – das Abstraktionsprinzip mit Logicly nutzend – die Entwicklung vom asynchronen RS-Latch bis zum D-Flipflop, welches wiederum als Basis für weitere Speicherbausteine dient. Diese Entwicklung ist für das Verständnis der Funktionsweise digitaler Speicherelemente von entscheidender Bedeutung und wird deshalb hier ausführlicher behandelt. Bei jeder Schaltung ist auch ein Zeitdiagramm vorhanden, um die unterschiedlichen Schaltverhalten in Abhängigkeit vom Taktsignal zu verdeutlichen. Das Taktsignal wird bei Logicly von einem Clock-Baustein geliefert. Bei diesem lässt sich auch die Zykluszeit einstellen.

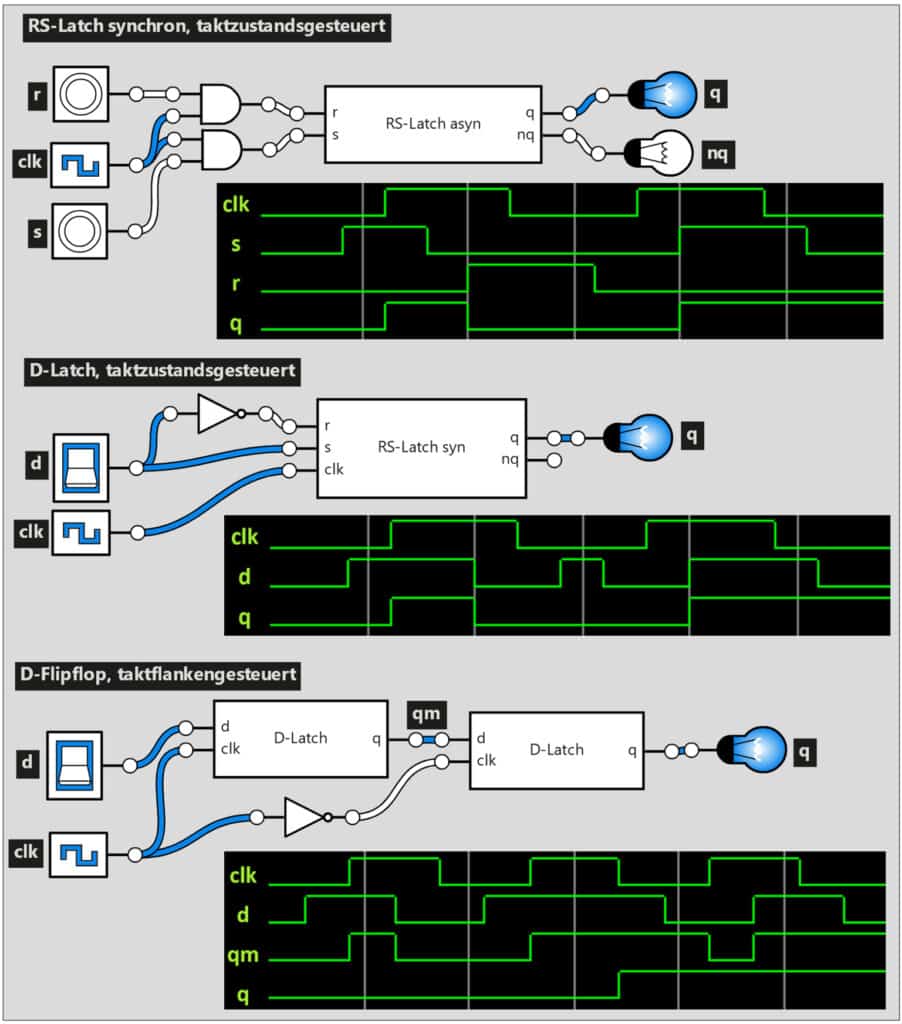
In der ersten Schaltung in Abb.23 wird das aus zwei NOR-Gattern bestehende asynchrone RS-Latch (vgl. Abb.22) in Form eines IC- Bausteins (RS-Latch asyn) zum Aufbau des synchronen RS-Latches genutzt. Dabei kommt zu den Eingängen r und s der clk-Eingang für das Taktsignal hinzu, welches mit r und s jeweils über ein UND- Gatter verknüpft ist. Dies sorgt dafür, dass das Latch nur während einer positiven Taktphase gesetzt oder rückgesetzt werden kann. Es wird daher auch als taktzustands- gesteuertes synchrones RS-Latch bezeichnet.

Das D-Latch in Abb.23 ist ebenfalls taktzustandsgesteuert. Im Gegensatz zum RS-Latch besitzt es neben dem Taktsignaleingang clk nur einen Eingang d. In der Schaltung wird das synchrone RS-Latch als IC (RS-Latch syn) genutzt. Dessen Eingänge r und s werden mit dem Signal d verbunden, wobei bei r ein NOT-Gatter vorgeschaltet ist. Bei d = 0 wird dadurch das Latch zurückgesetzt und bei d = 1 gesetzt. Das Signal d kann damit direkt den zu speichernden Bit-Wert repräsentieren.

Durch die Zustandssteuerung des D-Latches über die Taktphase wird zwar ein gewisser Grad an Synchronisation erreicht, bei Computersystemen ist es jedoch wichtig, potenzielle Zustandswechsel noch weiter einzuschränken. Genau dies erfolgt bei taktflankengesteuerten synchronen Speicherelementen, die einen Zustandswechsel nur noch während Taktflanken erlauben. Taktflankengesteuerte Speicherelemente werden als Flipflops bezeichnet.

Das D-Flipflop in Abb.23 ist negativ taktflankengesteuert, d.h. es kann seinen Zustand nur dann ändern, wenn sich das Taktsignal von 1 nach 0 ändert, sich also in der negativen oder fallenden Flanke befindet. Dieses Schaltverhalten wird erreicht, indem zwei D-Latch-ICs (D-Latch) hintereinandergeschaltet und mit inversen Taktsignalen betrieben werden. Das erste Latch wird als Master und das zweite Latch als Slave bezeichnet, die Schaltung wird deshalb auch Master-Slave-Flipflop genannt. Wird das Master-Latch mit dem inversen Taktsignal betrieben, ist die Schaltung positiv taktflankengesteuert, wird, wie in Abb.23, das Taktsignal des Slave-Latches invertiert, so ergibt sich ein negativ taktflankengesteuertes Flipflop. Im Zeitdiagramm des D- Flipflops ist zur Veranschaulichung der Funktionsweise auch der Verlauf des internen Signals qm enthalten. Es verbindet den Ausgang q des Master-Latches mit dem Eingang d des Slave-Latches.

Die Funktionalität des D-Flipflops erscheint auf den ersten Blick „etwas kläglich“. Es ist nur im Stande, den am Eingang d anliegenden Signalwert über einen Taktzyklus hinweg zu speichern.  Bei jeder nächsten steigenden bzw. fallenden Flanke des Taktsignals wird dieser Wert immer wieder neu eingelesen. Das D- Flipflop ist aber ein wichtiger Baustein, um weitere digitale Speicherelemente zu implementieren. Dies wird in Abb.24 gezeigt.

Zunächst muss dafür gesorgt werden, dass das D-Flipflop den d-Signalwert nicht nur über einen Taktzyklus hinweg speichert, sondern so lange wie dies benötigt wird. Diese Schaltung wird hier als 1-bit Register bezeichnet und ist in Abb.24 oben dargestellt. Die dauerhafte Speicherung wird hier durch die Verwendung eines 1-aus-2 Multiplexer-Bausteins (vgl. Abb.11) ermöglicht. Dieser versorgt bei sel=0 den d-Eingang des Flipflops immer mit wieder mit dessen Ausgangssignal q, also mit dem aktuell gespeicherten Wert. Bei sel=1 wird hingegen ein neuer Wert vom d-Eingang der Schaltung eingelesen. Der sel-Eingang des Multiplexers ist mit dem e-Eingang (enable) der Schaltung verbunden. Das dort anliegende Signal bestimmt also, ob das Register bei der nächsten steigenden bzw. fallende Flanke speichern (e=0) oder neu einlesen (e=1) soll.

Wird diese 1-bit Registerschaltung wiederum in einen IC-Baustein (Reg1) gepackt, so lassen sich damit n-bit breite Register zur Manipulation von n-bit Datenwörtern aufbauen. Abb.24 zeigt ein 4-bit Register als parallele Anordnung von vier dieser ICs, die hier negativ taktflankengesteuert synchron über eine gemeinsame Taktleitung (clk) und über eine gemeinsame Enable-Leitung (e) betrieben werden.

Wie schon erwähnt, lassen sich mit dieser parallelen Anordnung Register in beliebiger Breite erstellen. Werden mehrere Register kombiniert, kann ein Registersatz, auch Registerfile oder Registerbank genannt, aufgebaut werden. Derartige Registerstrukturen finden sich als sehr schnelle leistungsfähige Speicher im inneren Kern einer CPU.

Befehlszähler

Zählerbausteine stellen eine wichtige Klasse sequenzieller Standardkomponenten dar. Mit ihrer Hilfe lassen sich zeitlich aufeinanderfolgende Ereignisse registrieren oder auch erzeugen. Der Zählerstand muss dabei immer gespeichert werden.

In einem Computersystem ist der Befehlszähler oder Befehlszeiger (program counter  oder instruction pointer) eine Schlüsselkomponente, die den Von-Neumann-Zyklus antreibt. Er dient zur Adressierung des Programmspeichers und enthält zu jedem Zeitpunkt die Adresse der Speicherzelle mit dem nächsten auszuführenden Befehl. Die Programmbefehle sind zumeist nacheinander im Hauptspeicher abgelegt. Die sequenzielle Abarbeitung des Programms wird also erreicht, indem sich der Befehlszähler bei jedem Takt schrittweise erhöht. Bei Sprungbefehlen kann nicht einfach weiter gezählt werden. Dazu benötigt die Befehlszählerschaltung eine Lademöglichkeit, mit deren Hilfe der aktuelle Zählerstand mit einem extern angelegten Datenwort überschrieben werden kann. Ein Befehlszähler sollte überdies auch noch über einen eigenen Eingang für die Rücksetzung auf den Wert 0 verfügen.

Auch im Rahmen des „From Nand To Tetris“-Projekts soll für das zu erstellende virtuelle Computersystem eine Befehlszählerschaltung entwickelt werden. Diese Schaltung ist Teil der CPU. Abb.25 zeigt deren Spezifikation.

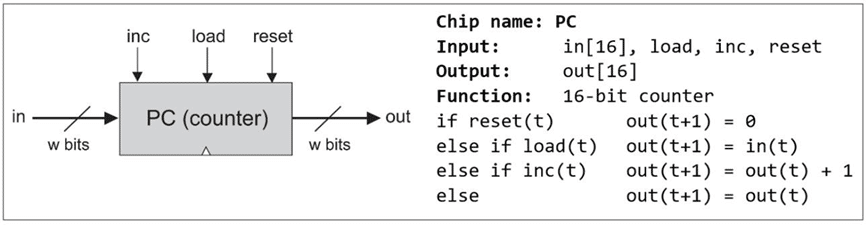
Abb.26  präsentiert eine mögliche schaltungstechnische Umsetzung dieser Spezifikation mit Logicly. Der Einfachheit halber als 4-bit-Version, im Original ist es ein 16-bit Befehlszähler.

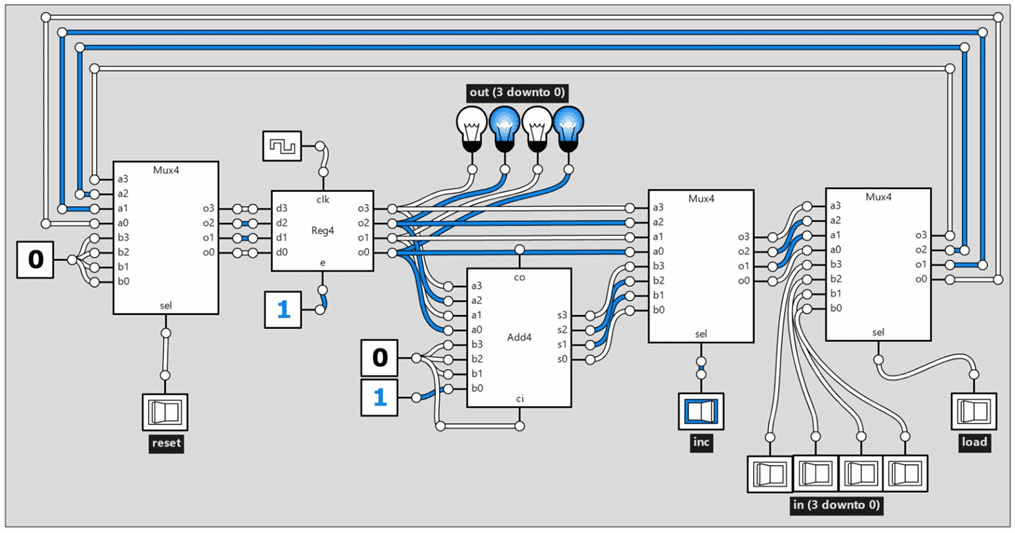
Die Schaltung enthält ein negativ taktflankengesteuertes Register (Reg4), einen Addierer (Add4) und drei 1-aus-2-Multiplexer (Mux4). Das Taktsignal für die gesamte Schaltung wird vom Clock-Baustein oberhalb des Registers geliefert. Das Register dient zum Speichern des aktuellen Zählerstandes. Dieser wird über die Light-Bulbs (o) angezeigt. Da der Enable-Eingang (e) des Registers fix auf den Wert 1 gesetzt ist, erfolgt die Speicherung des Zählerstandes immer nur über einen Taktzyklus hinweg. Entscheidend ist daher, welcher Signalwert bei jeder fallenden Taktflanke am Eingang anliegt.

Bei inc=0, load=0 und reset=0 wird der vom Register ausgegebene Wert wieder unverändert eingelesen und der Zählerstand bleibt gleich Bei inc=1, load=0 und reset=0 wird der vom Addierer um 1 erhöhte Zählerstand übermittelt, es wird also hinaufgezählt. Mit inc=0|1, load=1 und reset=0 wird der in-Signalwert eingelesen und weitergeleitet, der Zähler also auf diesen Wert gesetzt. Bei inc=0|1, load=0|1 und reset=1 wird der Zählerstand auf den Wert 0 zurückgesetzt. Für die Umsetzung der in der Spezifikation beschriebenen Priorität der Eingangssignale inc, load und reset ist die Abfolge der Multiplexer im Datenpfad der Schaltung entscheidend.

Abb.27 zeigt den Aufbau für die 16-bit Implementierung dieser Schaltung auf dem Terasic DE0-CV FPGA- Board.

Der Zählerstand wird im dezimalen Format (0 bis 65535) ausgegeben. Dazu werden fünf der sechs 7-Segment-Anzeigen des Boards genutzt. Für die Eingabe der Steuersignale inc, load und reset werden drei Switches verwendet. Deren Einstellung wird zusätzlich durch die darüber befindlichen LEDs angezeigt. Das Setzen des Zählers auf einen bestimmten Wert erfolgt über die Schnittstelle GPIO_1. Deren Pins sind über ein Flachbandkabel mit dem 40-Pin GPIO-Breakoutboard auf dem Steckbrett verbunden. Die Pins 1 bis 10 sowie 13 bis 18 des Breakoutboards sind an die zwei 8-poligen DIP-Schaltermodule auf dem Steckbrett angeschlossen. Pin 11 liefert 5V, Pin 29 liefert 3.3V und Pin 12 sowie Pin 30 liefern GND. Bei den DIP-Switches befinden sich masseseitig 100kΩ-Widerstände. Der FPGA-Chip stellt vier Taktsignale mit 50MHz zur Verfügung. Eines davon wird über einen Frequenzteiler verwendet, um für den Zähler ein Signal mit annähernd 1Hz zu erhalten.

Die weiteren Schritte entsprechen der schon bei der FPGA-Implementierung der ALU beschriebenen Vorgangsweise. Da es in erster Linie um die physische Umsetzung der entworfenen Schaltungen geht, wird aus didaktischen Gründen wiederum eine VHDL-Strukturbeschreibung verwendet. In der Praxis würde bei einem Befehlszähler ein Verhaltensmodell zur Anwendung kommen.

Abb.28 zeigt die verwendete VHDL-Beschreibung der Befehlszählerschaltung.

In der Entity-Definition werden die Ein- und Ausgänge des Befehlszählers definiert. Danach sind die Prototypen aller verwendeten Schaltungskomponenten (reg16, add16 und mux2way16) und die notwendigen Signalleitungen für deren Verbindung angeführt. Mit dem begin-Schlüsselwort wird die eigentliche Schaltungsbeschreibung eingeleitet. Hier werden die notwendigen Instanzen der Schaltungskomponenten erzeugt und mit den definierten Signalen sowie den Ein- und Ausgängen der Schaltung verbunden. Die einzelnen Schaltungskomponenten werden dabei in der gleichen Reihenfolge beschrieben, wie sie in Abb.26, von links nach rechts vorhanden sind.

In Abb.29 wird die VHDL-Beschreibung der Top-Level-Entity (pc_de0cv) zur Implementierung der Befehlszählerschaltung auf dem Terasic DE0-CV FPGA-Board wiedergegeben.

In der Entity-Definition in Abb.29 sind alle für die Befehlszählerschaltung verwendeten Board-Komponenten angeführt: die Taktsignalquelle (CLOCK_50), die GPIO-Schnittstelle (GPIO_1), die Switches (SW), die LEDs (LEDR) und die fünf 7- Segmentanzeigen (HEX0 bis HEX4). Die Zuordnung zwischen den für diese Komponenten verwendeten Kurzbezeichnungen und den betreffenden Pins auf dem FPGA-Chip wurde mit einer Assignment-Datei vorgenommen.

Bei den Schaltungskomponenten ist an erster Stelle eine Binärzählerschaltung (bincntr_g) angeführt. Diese dient zur Verringerung der von CLOCK_50 vorgegebenen Taktfrequenz von 50MHz auf etwa 1Hz. Die Variable n gibt dabei die Breite des Zählers in Bits an. Da es sich um eine sogenannte generische Komponentenbeschreibung handelt (generic), kann der Wert dieser Variablen auch noch weiter unten bei der Instanziierung angepasst werden. Die Komponente pc ist die eigentliche Befehlszählerschaltung, wie in Abb.28 beschrieben. Die beiden Schaltungskomponenten bin16tobcd und bcs2sseg dienen zur Umwandlung des binären Zählerwerts in das dezimale Format (Binary Coded Decimal) und dessen Anzeige auf den 7-Segment-Display-Bausteinen.

Nach der Definition der benötigten  Signalleitungen folgt die eigentlich Architekturbeschreibung.  Dabei werden Instanzen der Schaltungskomponenten erzeugt und mit den definierten Signalleitungen sowie den Board-Komponenten verbunden.

Nach der Kompilation der VHDL-Beschreibungen mit Quartus Prime und der Übertragung des erstellten Bitstreams auf das FPGA-Board sollte der Zähler bei eingeschaltetem inc-Switch von 0 beginnend automatisch hinaufzählen. Über den load-Switch kann der Zähler auf den an den DIP-Schaltern eingestellten Wert und bei aktiviertem reset-Switch auf den Wert 0 gesetzt werden (vgl. Abb.27).

So wie bei der FPGA-Implementierung der ALU bereits erwähnt, kann der im Unterricht notwendige Arbeitsaufwand für diese Implementierung durch den Einsatz von entsprechend vorinstallierten und vorkonfigurierten Systemen deutlich reduziert werden.

Schlusswort

Das hier vorgestellte didaktische und methodische Konzept zur Vermittlung von Grundlagen der Digitaltechnik endet mit der Vorstellung einer Befehlszählerschaltung „etwas willkürlich“. Dem Abstraktionsprinzip folgend wäre der Aufbau einer CPU-Schaltung ein möglicher nächster Schritt.

Das Design einer CPU wird in hohem Maße durch die abzubildende Computerarchitektur und die abzubildenden Maschinenbefehle, also durch den sogenannten Befehlssatz bestimmt. Die grundlegende Funktion einer CPU ist es, Maschinensprachenprogramme möglichst effizient auszuführen. Hier treffen Hard- und Software aufeinander. Schon bei der Entwicklung einer ALU, welche ein wesentlicher Bestandteil einer CPU ist, muss dies berücksichtigt werden.

Eine entsprechende Erörterung der Maschinensprachenprogrammierung im Allgemeinen und des in Betracht kommenden Befehlssatzes im Speziellen würde in diesem Beitrag, in dem es in erster Linie um die Vermittlung von Grundlagen der Digitaltechnik geht, wohl zu weit führen.

Eine mögliche Fortsetzung wäre die Vorstellung der Maschinensprache, der CPU und des damit aufgebauten Computersystems des „From Nand To Tetris“-Projektes. Wie schon erwähnt ist dieses Computersystem relativ einfach aufgebaut, aber leitungsfähig genug, um darauf Computerspiele wie Pong und Tetris mit Tastatureingabe und Bildschirmausgabe ausführen zu können.

Das „Form Nand To Tetris“-Projekt selbst sieht nur eine virtuelle Implementierung dieses Computersystems vor. Es wird in speziell dafür entwickelten Apps erstellt, getestet und genutzt. Im Zuge der Ausarbeitung des in diesem Beitrag vorgestellten Konzeptes konnte das „From Nand To Tetris“-Computersystem auch vollständig auf dem Terasic DE0-CV FPGA-Board implementiert werden.

In Abb.30 sind zwei Bildschirmausgaben des auf dem „From Nand To Tetris“-Computersystem laufenden Computerspiels PONG gegenübergestellt. Der Screenshot links stammt von der CPU-Emulator-App des Projekts. Das Foto rechts zeigt die von der erstellten FPGA-Implementierung erzeugte Ausgabe auf einem VGA-Bildschirm.

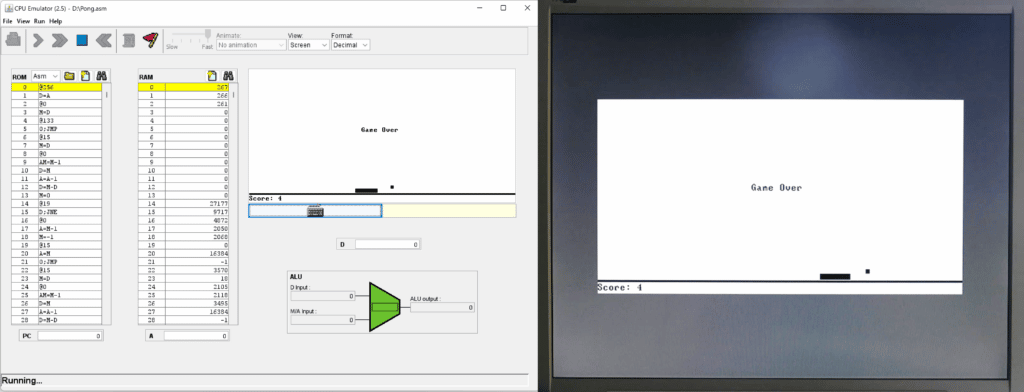
Wie schon in der Einleitung dieses Beitrags erwähnt, ist die aktive Auseinandersetzung mit der Digitaltechnik vor allem dann interessant und spannend, wenn dabei die mitunter bestechend einfachen logischen Zusammenhänge und Konzepte entdeckt und verstanden werden können, die sich hinter den komplizierten Strukturen moderner digitaler Systeme verbergen. Das ist natürlich ganz besonders der Fall, wenn man ein selbst programmiertes Computerspiel auf einem Computersystem spielt, das man auch selbst nur aus Logikgattern aufgebaut hat!

Im Rahmen des „From Nand To Tetris“-Projektes ist dies möglich. Ein wesentlicher Aspekt dabei ist das Prinzip der Abstraktion. Shimon Schocken, einer der Begründer dieses Projektes, weist in einem TED-Talk (https://www.ted.com/) in amüsanter Weise auf die besondere Bedeutung dieses Prinzips hin, indem er einen Ausschnitt von Michelangelos Meisterwerk an der Decke der Sixtinischen Kapelle in einer etwas modifizierten Form (vgl. Abb.31) mit den folgenden Worten präsentiert:

„So we start this journey by telling our students that God gave us Nand and told us
to build a computer, and when we asked how, God said, ‚One step at a time.'“

Literatur

• Cord, Elias: FPGAs für Maker. dpunkt, Heidelberg, 2016.
• Harris, Money David u. Sarah L. Harris: Digital Design and Computer Architecture. Elsevier, Boston. 2. Aufl. 2013.
• Himpe, Vincent: Digitale Logik selbst entwickeln. Elektor, Aachen, 2012.
• Hoffmann, W. Dirk: Grundlagen der technischen Informatik. Hanser, München, 6. Aufl. 2020.
• Kleitz, William: Digital Electronics with VHDL. Pearson, Essex, 2014.
• Nisan, Noam u. Shimon Schocken: The Elements of Computing Systems. Building a Computer from First Principles. MIT Press, Cambridge, 2. Aufl. 2021.
• Petzold, Charles: Code. The Hidden Language of Computer Hardware and Software. Microsoft Press, Redmond, 2013.
• Reichardt, Jürgen: Digitaltechnik. Eine Einführung mit VHDL. De Gruyter, Berlin, 4. Aufl. 2017.
• Rost, Manfred u. Sandro Wefel: Elektronik für Informatiker. De Gruyter, Berlin, 2. Aufl. 2021.
• Schulz, Peter u. Edwin Naroska: Digitale Systeme mit FPGAs entwickeln. Elektor, Aachen, 2016.

Links

• „Nand To Tetris“-Projektwebsite
• „Nand To Tetris“-MOOC, Teil 1
• „Nand To Tetris“-MOOC, Teil 2
• „Nand To Tetris“-TED-Talk
• Nandgame
• Logicly
• Tinkercad Circuits
• Terasic DE0-CV FPGA-Board
• Intel Quartus Prime Lite Edition Download
• Fritzing