Zeltlager
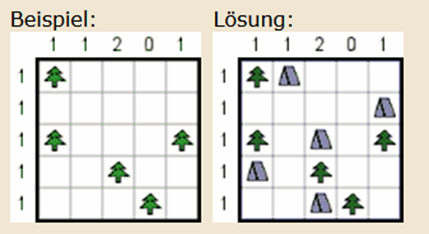
Dieses Rätsel schaut harmlos aus, hat es aber in sich. Die Aufgabe: in einem rechteckigen oder quadratischen Feld sind Bäume eingezeichnet.
- Zu jedem Baum ist genau ein Zelt daneben (das heißt links, rechts, oberhalb oder unterhalb des Baumes) aufzustellen.
- Zwei Zelte dürfen nicht waagrecht oder senkrecht nebeneinanderstehen. Diagonal ist erlaubt.
- In jeder Zeile und jeder Spalte ist angegeben, wie viele Zelte dort zu stehen haben.
Hier wieder ein Beispiel aus der schönen Sammlung von Angela und Otto Janko (https://www.janko.at/Raetsel/Zeltlager):
Datenstruktur
In den bisherigen Programmen wurde bisher der nächste level mit dem Eintragen einer gültigen Zahl (oder einer Königin) in ein Feld erreicht. Hier ist es sinnvoller. jedem Baum eine Nummer zuzuordnen, die gleich dem level ist, und den level nach der erfolgreichen Zuordnung eines Zelts zu erhöhen. Alle Felder werden wieder Spalte für Spalte und Zeile für Zeile nummeriert. Jeder Baum erhält eine Platznummer, aus der seine Koordinaten Zeile (r) und Spalte (c) errechnet werden. Mit moves werden jene Plätze bestimmt, auf die ein Zelt gestellt werden kann. valid prüft, ob dabei die Bedingungen eingehalten werden. Die Hilfsfunktion neighbors bestimmt zu einer Feldnummer die Nummern der Nachbarn, also aller horizontal und vertikal (aber nicht diagonal) umgebenden Felder.
Das Beispiel oben enthält 25 Felder (von 0 bis 24 nummeriert). Die Bäume stehen auf den Feldern 0, 10, 14, 17 und 23. Diese Nummern werden als Liste trees gespeichert. Nachbarn von 10 wären beispielsweise 5, 11 und 15. Die geforderte Anzahl der Zelte wäre in den Zeilen (rows) 1, 1, 1, 1, 1 und in den Spalten (cols) 1, 1, 2, 0, 1. Somit wird dieses Rätsel durch die drei Listen
trees = [0, 10, 14, 17, 23]
rows = [1, 1, 1, 1, 1]
cols = [1, 1, 2, 0, 1]
beschrieben.
zeltlager.py
# File zeltlager.py
from backtrack import Backtrack
class Zeltlager(Backtrack):
trees = [0, 10, 14, 17, 23]
rows = [1, 1, 1, 1, 1]
cols = [1, 1, 2, 0, 1]
# Auch rechteckige Plätze sind möglich, daher zwei Größenangaben
rsize = len(rows)
csize = len(cols)
tents = [] # Zu Beginn sind keine Zelte aufgebaut
solutionNr = 0 # Nummer der Lösung
rowscount = [0 for i in range(rsize)] # Aktuelle Anzahl der Zelte pro Zeile
colscount = [0 for i in range(csize)] # Aktuelle Anzahl der Zelte pro Spalte
def __init__(self, test:bool= False, showAttempts:bool = False):
super().__init__(test, showAttempts)
def rowAndCol(self, where:int) -> tuple:
s = self.rsize
return (where // s, where % s)
def neighbors(self, place:int) -> list[int]:
r, c = self.rowAndCol(place)
s = self.rsize
n = [ ]
if c+1<s:
n.append(place+1)
if r>0:
n.append(place-s)
if c>0:
n.append(place-1)
if r+1<s:
n.append(place+s)
return n
def moves(self, level: int) -> list[int]:
return self.neighbors(self.trees[level])
def valid(self, level: int, move:int) -> bool:
if move in self.trees: # da steht ein anderer Baum
return False
if move in self.tents: # da steht schon ein zelt
return False
for n in self.neighbors(move):
if n in self.tents: # da steht schon ein Zelt daneben
return False
r, c = self.rowAndCol(move)
if self.rowscount[r] >= self.rows[r]: # kein weiteres Zelt möglich
return False
if self.colscount[c] >= self.cols[c]: # kein weiteres Zelt möglich
return False
return True
def record(self, level: int, move:int):
self.tents.append(move)
r, c = self.rowAndCol(move)
self.rowscount[r] += 1
self.colscount[c] += 1
def undo(self, level: int, move:int):
self.tents.pop()
r, c = self.rowAndCol(move)
self.rowscount[r] -= 1
self.colscount[c] -= 1
def done(self, level: int)-> bool:
if len(self.trees) == len(self.tents):
self.solutionNr += 1
self.show()
return True
return False
def show(self):
# Einfache Ausgabe:
# print(f“\nSolution {self.solutionNr:4} level={level} {self.tents}“)
# Schönere Ausgabe:
tree = "B" # B steht für Baum
tent = "Z" # Z steht für Zelt
print(f"\nLösung {self.solutionNr:4}")
print(" "*6, end="")
for c in range(self.csize):
print(f"{self.cols[c]:3}", end="")
print()
for r in range(self.rsize):
print(f"{self.rows[r]:2d} -> ", end="")
for c in range(self.csize):
f = r*self.rsize + c # Feldnummer
if f in self.trees:
print(f" {tree}", end="")
elif f in self.tents:
print(f" {tent}", end="")
else:
print(" .", end="")
print()
if __name__ == "__main__":
Zeltlager(test=False, showAttempts=True)
Ergebnisse
Das Programm (zeltlager.py) findet zwei Lösungen, hier mit den Randbeschriftungen:
Lösung 1
1 1 2 0 1
1 -> B Z . . .
1 -> Z . . . .
1 -> B . Z . B
1 -> . . B . Z
1 -> . . Z B .
Lösung 2
1 1 2 0 1
1 -> B Z . . .
1 -> . . . . Z
1 -> B . Z . B
1 -> Z . B . .
1 -> . . Z B .
44 attempts in 0.50 seconds
B steht Baum und Z für Zelt. Nette Symbole aus dem Unicode-Zeichensatz wären besser, erfordern aber mehr Aufwand, da sie keine einheitliche Zeichenbreite aufweisen.
zeltlager_2.py zeigt ein anderes Beispiel, wieder mit der Übergabe der Problembeschreibung als Argumente an Zeltlager.
zeltlager_3.py enthält eine neue Angabe für eine schwierige Aufgabe. Die Lösungen 2 und 3 sehen gleich aus. Allerdings werden Bäume und Zelte unterschiedlich zugeordnet. Um das anzuzeigen, wird hier anstelle von „Z“ die Nummer des Baums angezeigt, der zu dem Zelt gehört. Das zeigt, dass in den Lösungen 2 und 3 die Baumnummern 11 und 14 vertauscht sind.
Links
- Alle Dateien
- Was ist eigentlich ‚Backtracking‘? (clubcomputer.at)
- Backtracking: Königinnenproblem (clubcomputer.at)
- Backtracking: Sudoku (clubcomputer.at)
- Backtracking: Kendoku (clubcomputer.at)
- Backtracking: Skyline (clubcomputer.at)
- Backtracking: Zeltlager (clubcomputer.at)
Martin Weissenböck hat die HTL 3 Rennweg 23 Jahre lang geleitet, schreibt Skripten, Lehrbücher und Artikel für die PCNEWS, leitet die Arbeitsgemeinschaft für Didaktik, Informatik und Mikroelektronik (ADIM) und den Verein SCHUL.InfoSMS. Er hält Vorträge und ist Lehrbeauftragter an der Technischen Universität Wien.

Neueste Kommentare